Question

Пожарное ведро имеет форму конуса. Его наклонная равна 41 см, а сумма
высоты и радиуса – 49 см. Найдите объём ведра

Answer 1

Ответ:

1080 π см ³ или  4800π см ³.

Пошаговое объяснение:

Пожарное ведро имеет форму конуса. Его наклонная равна 41 см, а сумма высоты и радиуса - 49 см. Найти объем ведра.

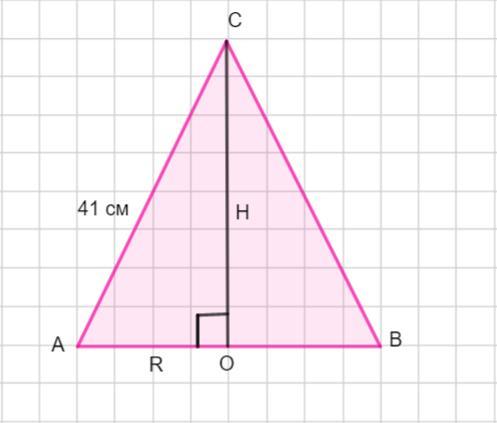
Рассмотрим осевое сечение конуса - равнобедренный ΔАВС.

Образующие АС =ВС =41 см. СО -высота, АО - радиус основания конуса.

По условию СО +АО =49см.

Рассмотрим ΔАОС - прямоугольный.

Пусть радиус АО =х см. Тогда высота СО =(49 -х) см.

Составим уравнение, воспользовавшись теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AC^{2} =AO^{2} +CO^{2} ;\\x^{2} +(49-x)^{2} =41^{2} ;\\x^{2} +49^{2} -98x+x^{2} =41^{2} ;\\2x^{2} -98x+2401-1681=0;\\2x^{2} -98x+720=0|:2\\x^{2} -49x+360=0;\\D =(-49)^{2} -4\cdot 1\cdot 360=2401- 1440=961=31^{2} ;\\\\x{_1}= \dfrac{49-31}{2} =\dfrac{18}{2} =9;\\\\x{_1}= \dfrac{49+31}{2} =\dfrac{80}{2} =40$

В первом случае R= AO= 9cм, тогда Н =СО = 49- 9 =40 см ;

Во втором случае R= AO= 40cм, тогда Н =СО = 49- 40 =9 см.

Объем конуса определяется по формуле

$V= \dfrac{1}{3} \pi R^{2} \cdot H$

Найдем объем для каждого случая

1) $V= \dfrac{1}{3} \pi\cdot 9^{2} \cdot 40=3\cdot 9\cdot 40 \pi =1080\pi$ см ³

2) $V= \dfrac{1}{3} \pi\cdot 40^{2} \cdot 9=3\cdot 1600 \pi =4800\pi$ см ³.

#SPJ1