Предмет: Геометрия,
автор: rook35728
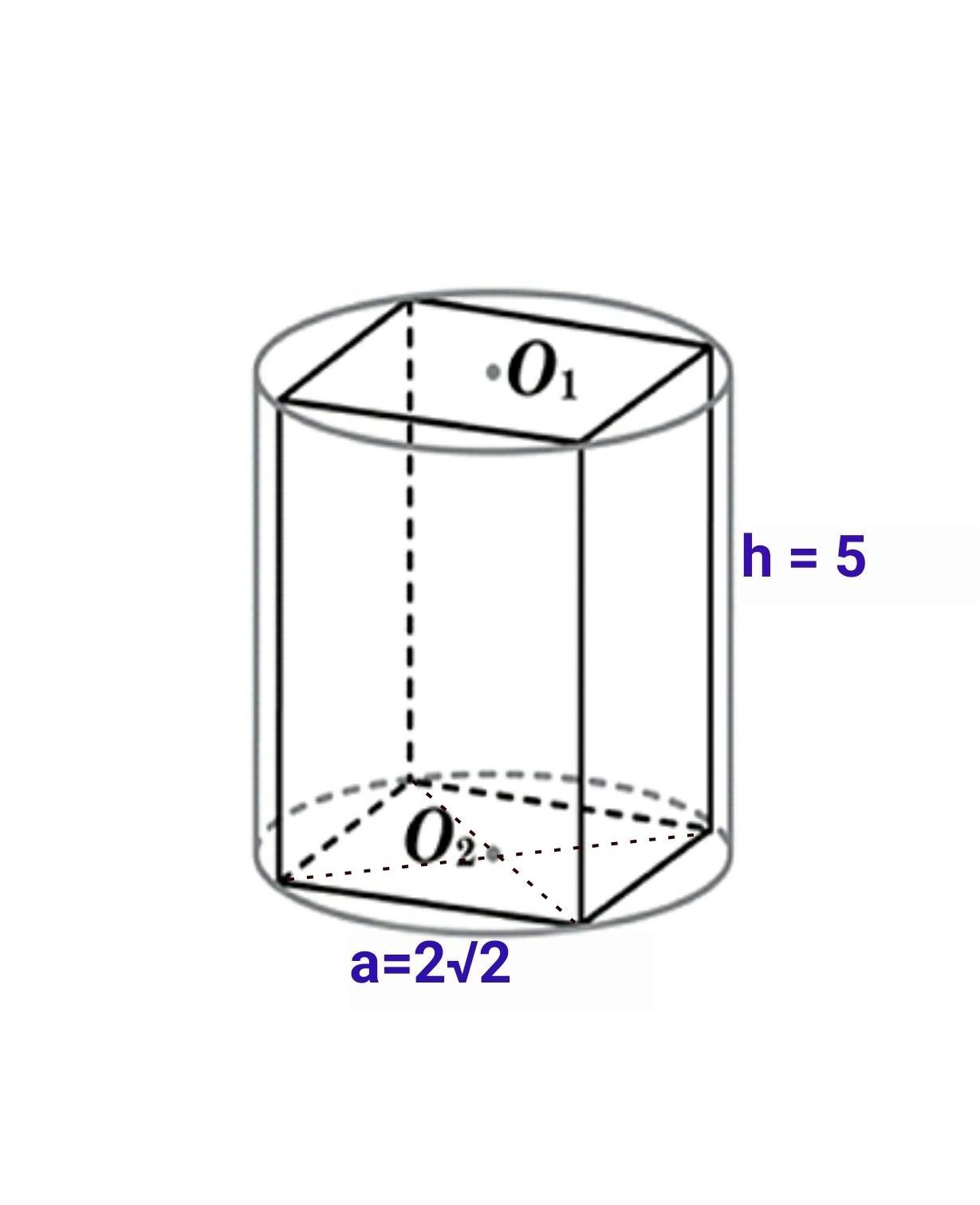
В правильній чотирикутній призмі сторона основи дорівнює 2√2 см, а висoтa 5 см. Знайдіть об'єм циліндра, описаного навколо призми.
З малюнком
Ответы
Автор ответа:
2
Ответ:
Об'єм циліндра дорівнює 20π см³
Объяснение:
В правильній чотирикутній призмі сторона основи дорівнює 2√2 см, а висoтa 5 см. Знайдіть об'єм циліндра, описаного навколо призми.
Якщо радіус циліндра дорівнює R, а висота h, то об'єм циліндра:
V=πR²h
1.
В основі правильної чотирикутної призми лежить квадрат зі стороною а=2√2 см. В основі циліндра лежить коло, яке описано навколо квадрата.
Радіус циліндра збігається з радіусом описаного навколо квадрата кола.
- Радіус кола описаного навколо правильного чотирикутника обчислюється за формулою:
Маємо:
(см)
2.
Висота циліндра збігається з висотою циліндра, h=5 см.
Отже, знайдемо об'єм циліндра:
V=π•2²•5=20π см³
Відповідь: 20π см³
#SPJ1
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: iiisis
Предмет: Английский язык,
автор: mironoksi32
Предмет: Английский язык,
автор: lebedevamirraslava
Предмет: Математика,
автор: oksanabelousova778
Предмет: Информатика,
автор: V9ova