Предмет: Геометрия,
автор: nikolaukuznecov
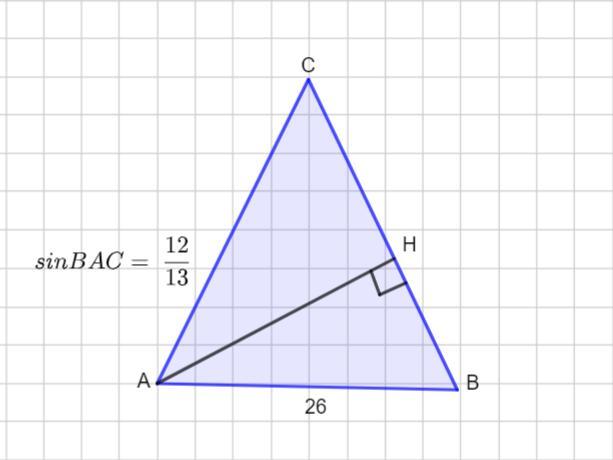
В треугольнике ABC AC=BC, AH-высота,AB=26,sin BAC=12/13.Найти BH
Ответы
Автор ответа:
9
Ответ:
BH =50 ед .
Объяснение:
В треугольнике АВС АС =ВС, АН -высота , АВ =26 , sinBAC =12/13.Найти ВН.
Пусть дан Δ АВС - равнобедренный, так как АС =ВС . В нем проведена высота АН.
В равнобедренном треугольнике углы при основании равны:
∠А =∠В.
Тогда sin BAC= sin ABC = 12/13.
Рассмотрим Δ АНВ - прямоугольный, так как АН - высота
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Найдем ВН по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: gorob29
Предмет: География,
автор: Аноним
Предмет: Қазақ тiлi,
автор: lizazalizaza531
Предмет: Английский язык,
автор: bewag71584