Предмет: Алгебра,
автор: kokhanevychdmytro
найти площадь фигуры ограниченной астроидой x=a cos(t)^3 y= b sin(3t)^3
Приложения:
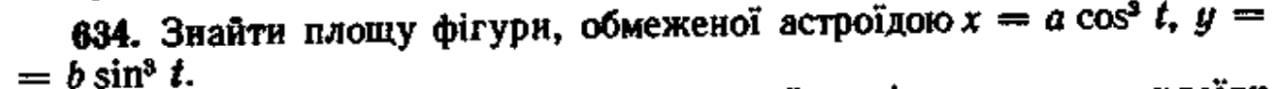
Ответы
Автор ответа:
0
S = ∫[a,b] y dx,
x = a cos(t)^3,
y = b sin(3t)^3,
S = ∫[t1,t2] x dy,
S = ∫[0,2π] a cos(t)^3 * 3b sin(3t)^2 cos(t) dt
S = 3ab∫[0,2π] cos^4(t) sin^2(3t) dt
S = 3ab∫[0,2π] (1-sin^2(t))^2 sin^2(3t) dt
S = 3ab∫[0,2π] (sin^6(t) - 2sin^4(t) + sin^2(t)) sin^2(3t) dt
S = 3ab ( [sin^7(t)/7 - 2sin^5(t)/5 + sin^3(t)/3]sin^3(3t)/9 |0 to 2π )
S = 81abπ/35
Похожие вопросы
Предмет: Английский язык,
автор: kirillkramskoj77
Предмет: Музыка,
автор: max555666
Предмет: Математика,
автор: patelidanil
Предмет: Английский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: tomiriszhaqsylyq