Предмет: Алгебра,
автор: lerak8340
ДОПОМОЖІТЬ, БУДЬ ЛАСКА!!!! ДАЮ 50 БАЛІВ!
Приложения:
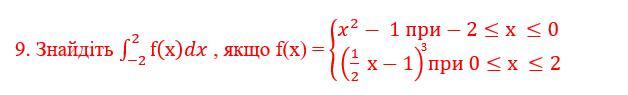
Ответы
Автор ответа:
1
Ответ:
Применим свойство аддитивности определённого интеграла . Оно состоит в том, что если промежуток интегрирования разбить на две части, то определенный интеграл по всему промежутку будет равен сумме двух определенных интегралов по частичным промежуткам.
Похожие вопросы
Предмет: История,
автор: azidkova682
Предмет: Химия,
автор: pyrogov11
Предмет: История,
автор: manasbekusuf
Предмет: Обществознание,
автор: caralin14
Предмет: Математика,
автор: mozonlil