Question

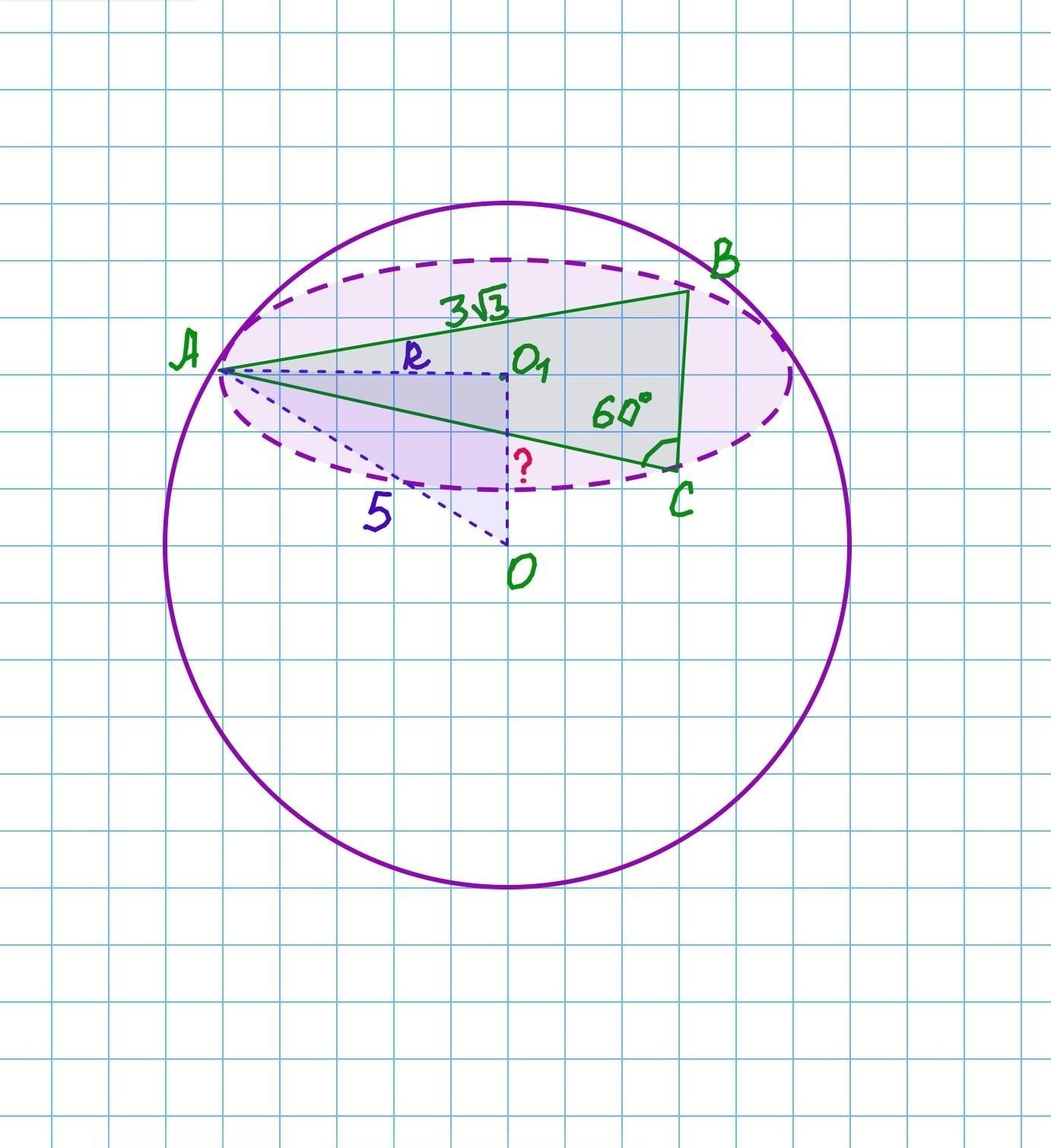
сторона трикутника, що лежить проти кута 60 градусів дорівнює 3√3. Усі вершини трикутника належать сфері. Знайдіть відстань від центра сфери до площини трикутника, якщо радіус сфери дорівнює 5 см.

Answer 1

Ответ:

Відстань від центра сфери до площини трикутника дорівнює 4 см

Объяснение:

Сторона трикутника, що лежить проти кута 60 градусів дорівнює 3√3. Усі вершини трикутника належать сфері. Знайдіть відстань від центра сфери до площини трикутника, якщо радіус сфери дорівнює 5 см.

Маємо сферу з центром в точці О і радіусом 5 см та △АВС зі стороною АВ=3√3 см, ∠С=60°, вершини якого лежать на сфері.

1.

За властивістю: через три точки можна провести площину, ця площина перетинає сферу по колу з центром в точці О1, яке описано навколо трикутника АВС.

АО1=R - радіус кола.

Оскільки вершини △ABC лежать на сфері, то АО - радіус сфери. AO=5 см.

ОО1 - відстань від центра сфери до площини трикутника АВС ⇒ ОО1 ⟂ (АВС), зокрема ОО1⟂АО1.

Відстань ОО1 будемо знаходити з прямокутного трикутника АОО1.

2.

Для цього необхідно знати АО1, яка являється радіусом описаного навколо трикутника АВС кола.

Згідно з узагальненою теоремою синусів:

$\dfrac{AB}{sin\angle C} = 2R$

маємо:

$AO_1 = R = \dfrac{AB }{2 \times sin 60^\circ} = \dfrac{3 \sqrt{3} }{ 2 \times \frac{ \sqrt{3} }{2} } = \bf 3$ (см)

3.

З прямокутного трикутника АО1О по теореме Пифагора знайдемо катет ОО1:

$OO_1= \sqrt{ {AO}^{2} - {AO_1}^{2} } = \sqrt{ {5}^{2} - {3}^{2} } = \sqrt{25 - 9} = \bf 4$ (см)

Відповідь: 4 см

#SPJ1