Question

У кулю вписано конус, площа бічної поверхні якого дорівнює $8\pi \sqrt3$ см$^{2}$, а твірна нахилена до площини основи під кутом 30°. Знайдіть об’єм цієї кулі.

Answer 1

Ответ:

Объем шара равен  256π/3 см³

Объяснение:

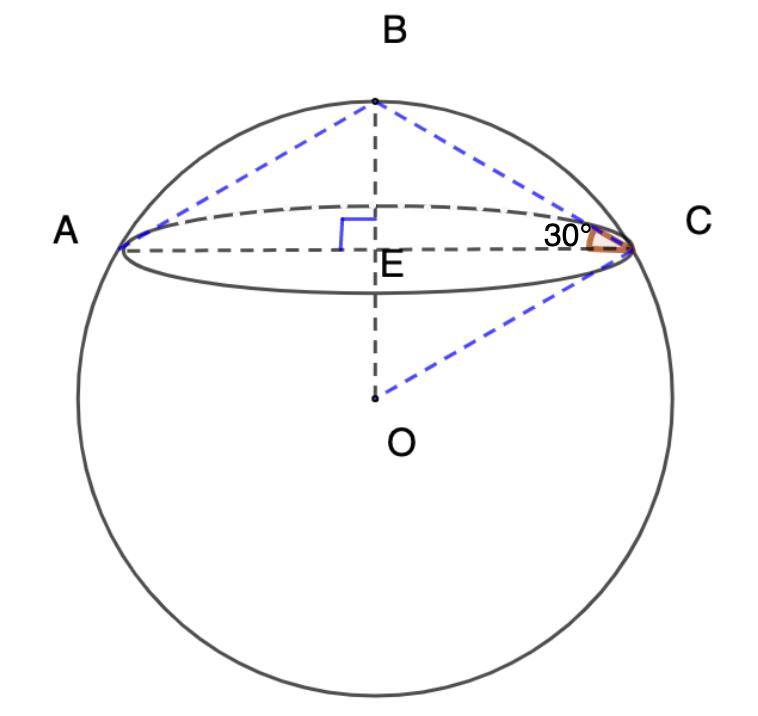
В шар вписан конус, площадь боковой поверхности которого равна 8π√3 см², а образующая наклонена к плоскости основания под углом 30°. Найдите объем этого шара.

Дано: Шар.О;

Конус вписан в шар.

Sбок. = 8π√3 см²;

Найти: Vшара.

Решение:

• Осевое сечение конуса - равнобедренный треугольник.

ВЕ - высота.

Рассмотрим ΔЕВС - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

∠ЕСВ = 30°   ⇒   ∠ЕВС = 90° - 30° = 60°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

Пусть ВЕ = х см, тогда ВС = 2х см

По теореме Пифагора:

ЕС² = ВС² - ВЕ² = 4х² - х² = 3х²   ⇒   ЕС = х√3 см

• Площадь боковой поверхности конуса равна:

                  Sбок. = πRl ,

где R - радиус основания конуса, l - образующая.

У нас R = EC = х√3 см;   l = BC = 2x см;   Sбок. = 8π√3 см

Подставим эти данные в формулу:

8π√3 = π · х√3 ·2х

8π√3 = 2х²π√3

х² = 4

х = 2

⇒ ВС = 4 см.

Рассмотрим ΔОВС

ОВ = ОС = R шара

⇒  ΔОВС - равнобедренный

∠ЕВС = 60°

• Если в равнобедренном треугольнике есть угол 60°, то он равносторонний.

⇒ ВС = ОВ = ОС = 4 см.

Радиус шара равен 4 см, можем найти объем.

            V шара = 4/3 πR³

⇒ V шара = 4/3 π · 4³ = 256π/3  (см³)

#SPJ1