помогите пожалуйста
решите уравнение:
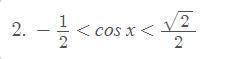
Ответы
Ответ:
Пошаговое объяснение:
Щоб знайти розв'язок нерівності -1/2 < cos x < √2/2, ми можемо використати геометричний підхід та скористатися графіком функції косинуса. Косинус x - це координата точки на колі з одиничним радіусом, яка лежить на відрізку, що проходить від початку координат до точки з координатами (cos x, sin x).
Таким чином, нерівність -1/2 < cos x < √2/2 можна інтерпретувати як обмеження на значення косинуса x, тобто точки на колі з одиничним радіусом, які лежать між двома горизонтальними прямими, які перетинають коло на відстані -1/2 та √2/2 від початку координат відповідно.
Отже, ми повинні знайти всі кути x, для яких координата x точки на колі з одиничним радіусом лежить між -1/2 та √2/2. Ці значення можуть відповідати двом частинам кола: одній частині між точками з координатами (-1/2, -√3/2) та (√2/2, √2/2) та іншій частині між точками з координатами (-√2/2, -√2/2) та (1/2, √3/2).
Таким чином, розв'язок нерівності -1/2 < cos x < √2/2 складається з усіх кутів, які відповідають цим двом частинам кола, тобто:
-π/3 < x < π/4 або 5π/4 < x < 4π/3
де -π/3 та π/4 є кутами, які відповідають точкам (-1/2, -√3/2) та (√2/2, √2/2), а 5π/4 та 4π/3 є кутами, які відповідають точкам (-√2/2, -√2/2) та (1/2, √3/2).