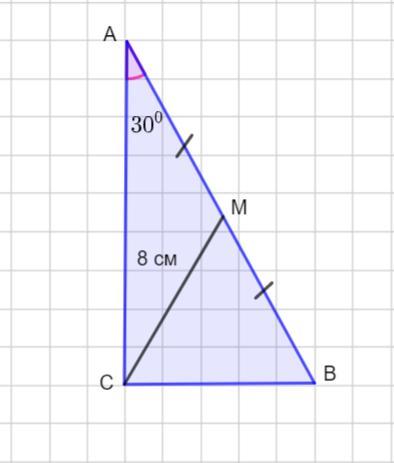
в прямокутному трикутнику медіана, проведена до гіпотенузи, становить 8 см, а один з гострих кутів 30 градусів. яка площа трикутника?
срочно даю 15 балов нужно полное решение
Ответы
Ответ:
32√3 см²
Объяснение:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна 8 см, а один из острых углов равен 30 градусов. Какая площадь треугольника.
Пусть дан Δ АВС -прямоугольный, так как ∠С =90 °. В треугольнике проведена к гипотенузе медиана СМ, СМ = 8 см. Так как в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине, то АВ = 2·8 =16 см.
∠А =30 °. В прямоугольном треугольнике катет, лежащий напротив угла в 30°, равен половине гипотенузы. Тогда ВС = 16:2 =8 см.
Найдем катет АС по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
АС =√(16²-8²)=√(16-8)(16+8)=√(8·24)=8√3 см.
Площадь прямоугольного треугольника равна полупроизведению катетов.
Площадь прямоугольного треугольника равна 32√3 см²
#SPJ1