Предмет: Математика,
автор: petrzadoyanchuk
математический анализ
Приложения:
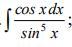
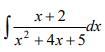
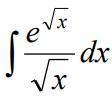
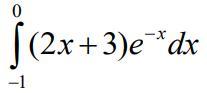
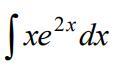
Ответы
Автор ответа:
0
Ответ:
1)
2)
3)
4)
5)
Примечание:
По таблице интегралов:
По свойствам интегралов:
Интегрирование по частям:
функции от аргумента x
Пошаговое объяснение:
1)
2)
3)
4)
а)
-----------------------------------------------------------------------------
-----------------------------------------------------------------------------
б)
в)
5)
-----------------------------------------------------------------------------
-----------------------------------------------------------------------------
Похожие вопросы
Предмет: Қазақ тiлi,
автор: merejbek17000
Предмет: Математика,
автор: ismagambetovy
Предмет: Математика,
автор: taa304795
Предмет: Химия,
автор: aniatkachuk2006
Предмет: История,
автор: masha8538