Question

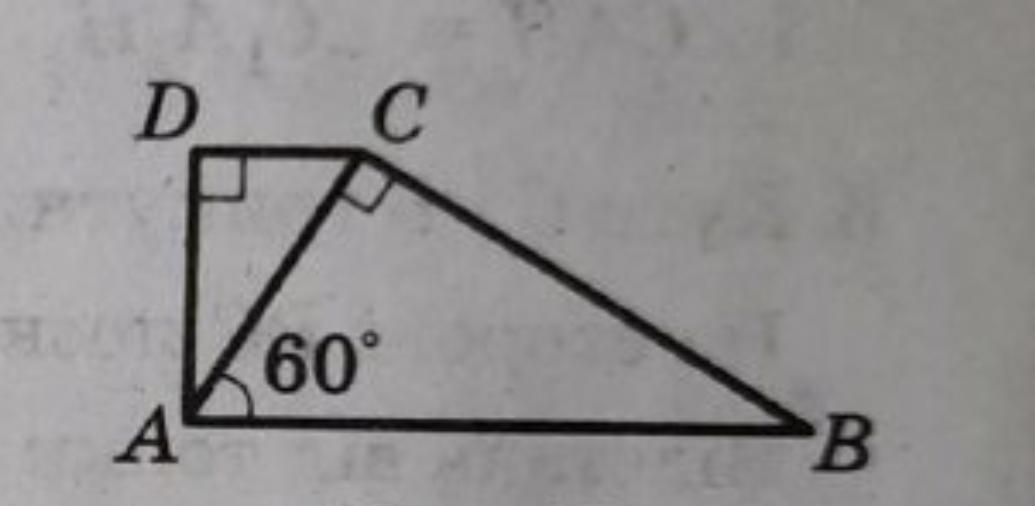
На рисунку ∠АСВ=90°, ∠ADC=90°, ∠BAC=60°. Знайдіть кут ACD, якщо АВ=4 см, СD=1 cм.

Answer 1

Ответ:

∠ACD=60°

Объяснение:

На рисунку ∠АСВ=90°, ∠ADC=90°, ∠BAC=60°. Знайдіть кут ACD, якщо АВ=4 см, СD=1 cм

• Якщо у прямокутному трикутнику один з гострих кутів дорівнює 30°, то катет протилежній цьому куту буде дорівнювати половині гіпотенузі.
• Косинусом гострого кута прямокутного трикутника називають відношення прилеглого катета до гіпотенузи.

1. У прямокутному  АВС(∠АСВ=90°) за теоремою про суму гострих кутів прямокутного трикутника, знайдемо ∠В:

∠В=90°-∠BAC=90°-60°=30°

Катет АС лежить проти кута ∠В=30°, тому за властивістю він дорівнює половині гіпотенузи АВ:

АС= 1/2 · АВ = 1/2 ·4 = 2 (см)

2. Розглянемо прямокутний трикутник ACD

За означенням косинуса гострого кута прямокутного трикутника маємо:

$\sf \cos\angle ACD=\dfrac{CD}{AC} =\dfrac{1}{2}$

Отже, ∠ACD=60°

#SPJ1