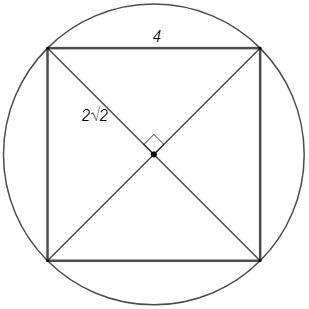
Площа квадрата, вписаного в коло, дорівнює 16 см². Знайдіть площу сегмента, основою якого є сторона квадрата.
Ответы
Ответ:
Объяснение:
Площадь квадрата, вписанного в круг, равна 16 см². Найти площадь сегмента, основанием которого является сторона квадрата.
1. Находим сторону квадрата: S=a² => a=√S = √16 = 4 (см)
2. Находим диагональ квадрата, которая является диаметром описанного круга:
D²=2a² => D=√(2a²) = √32 = 4√2 (см)
3. Находим площадь круга:
S₁= 1/4 πD² = 8π = 25,12 (см²)
4. Площадь четырех искомых сегментов круга равна разности между площадью круга и площадью вписанного квадрата:
4S' = S₁ - S = 25,12 - 16 = 9,12
S' = 9,12 : 4 = 2,28 (см²)
Ответ: 2,28 см²
Сторона квадрата √16=4, диагональ 4√2
Радиус - половина диагонали, 2√2
Угол сегмента - между диагоналями, 90°
S_сегм = R^2/2 (ф-sinф) // ф в радианах
= 4(п/2 -1) =2п-4 (см^2)