Question

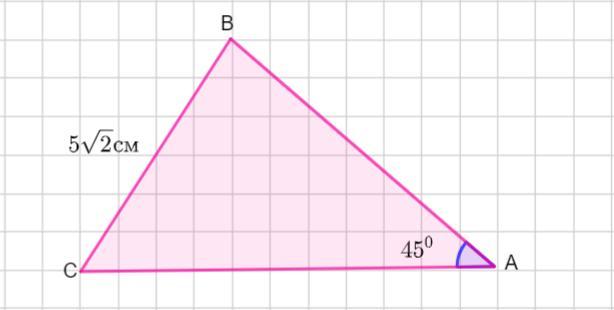
в трикутнику одна сторона дорівнює 5√2 см, а протилежний кут дорівнює 45°. Знайдіть довжину радіуса описаного кола.

Answer 1

Ответ:

5 см

Объяснение:

В треугольника одна сторона равна 5√2 см, а противолежащий угол равен 45°. Найти длину радиуса описанной окружности.

Пусть дан ΔАВС , ∠А =45 °, а противолежащая сторона ВС =5√2 см.

Радиус окружности, описанной около треугольника определяется по формуле:

$R =\dfrac{a}{2sin\alpha } ,$  где а - сторона треугольника, противолежащая к углу α.

Тогда получим

$R =\dfrac{BC }{2sin A} ;\\\\R =\dfrac{5\sqrt{2} }{2sin 45^{0} }$

Так как

$sin45^{0} =\dfrac{\sqrt{2} }{2} ,$

то

$R =\dfrac{5\sqrt{2} }{2\cdot \dfrac{\sqrt{2} }{2} }=\dfrac{5\sqrt{2} }{\sqrt{2} } =5$

Значит, радиус окружности описанной около треугольника равен

5 см

#SPJ1