Предмет: Геометрия,
автор: julia1160
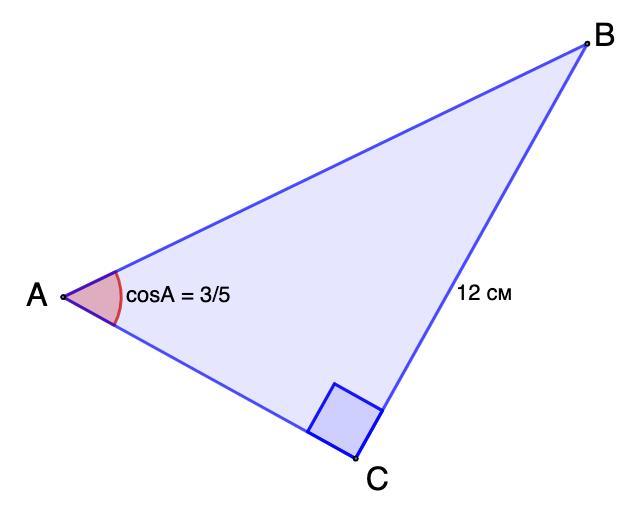
У трикутнику ABC |_C = 90º, BC = 12 см, cos A = 3/5 . Знайдіть периметр трикутника.
Ответы
Автор ответа:
4
Ответ:
Периметр треугольника равен 36 см.
Объяснение:
В треугольнике ABC ∠C = 90º, BC = 12 см, cos А = 3/5 . Найдите периметр треугольника.
Дано: ΔАВС - прямоугольный;
∠C = 90º, BC = 12 см,
cos А = 3/5.
Найти: Р(АВС)
Решение:
- Косинус угла - отношение прилежащего катета к гипотенузе.
⇒
Пусть АС = 3х см, тогда АВ = 5х см.
- Теорема Пифагора - квадрат гипотенузы равен сумме квадратов катетов.
⇒ АВ² = АС² + ВС²
25х² = 9х² + 144
16х² = 144 |:16
x² = 9
x = 3
⇒ АС = 9 см; АВ = 15 см
- Периметр - сумма длин всех сторон.
Р(АВС) = АВ + ВС + АС = 15 + 12 + 9 = 36 (см)
Периметр треугольника равен 36 см.
#SPJ1
Приложения:
julia1160:
Спасибо большое, но мне уже не надо
Другим понадобится)
Похожие вопросы
Предмет: Русский язык,
автор: akzhan45
Предмет: Английский язык,
автор: smartlucifer
Предмет: Алгебра,
автор: emaosa003
Предмет: Математика,
автор: Аноним
Предмет: Информатика,
автор: veronikanicanika