Question

срочно пожалуйста )! дам 38 балов


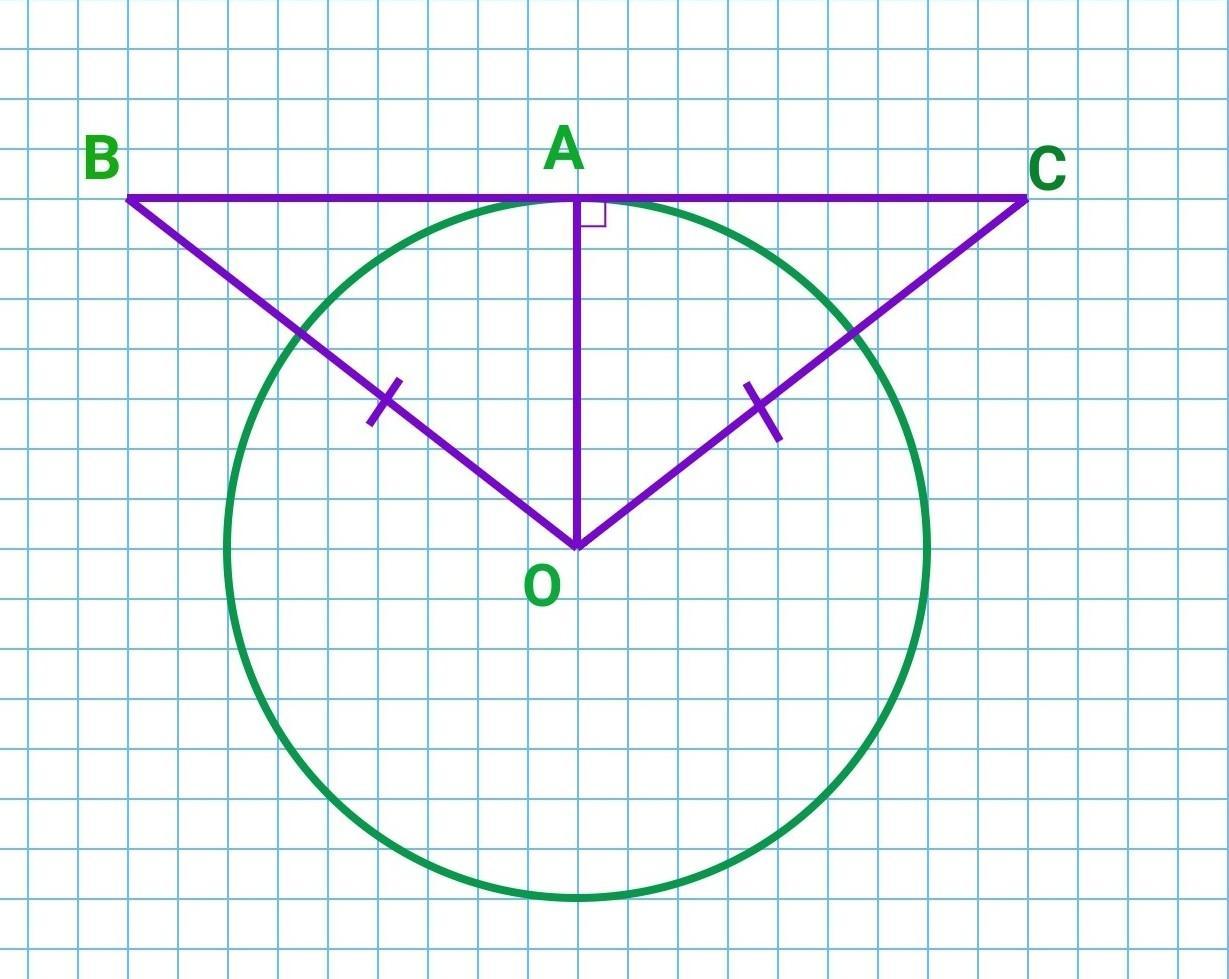
Пряма дотикається кола з центром О в точці А. На дотичній по різні сторони від точки А позначили точки В іС такі,що ОВ=ОС. Доведіть , що ВА=АС.


( сделайте пожалуйста рисунок , это обязательно )

Answer 1

Ответ:

Довели, що ВА=АС

Объяснение:

Пряма дотикається кола з центром О в точці А. На дотичній по різні сторони від точки А позначили точки В і С такі,що ОВ=ОС. Доведіть , що ВА=АС.

Властивість дотичної:

Дототична до кола перпендикулярна до радіуса, проведеного в точку дотику.

Доведення

Маємо коло з центром в точці О. Пряма ВС дотикаються до кола в точці А. ОА - радіус кола.

За властивістю дотичної ВС⟂АО. Отже, ∠ОАВ=∠ОАС=90°.

Розглянемо прямокутні трикутники ОАВ і ОАС.

• ОВ=ОС - за умовою
• ОА - спільна

Звідси, △ОАВ=△ОАС за гіпотенузою і катетом.

АВ=АС - як відповідні сторони рівних трикутників, що и треба було довести.

#SPJ1