Question

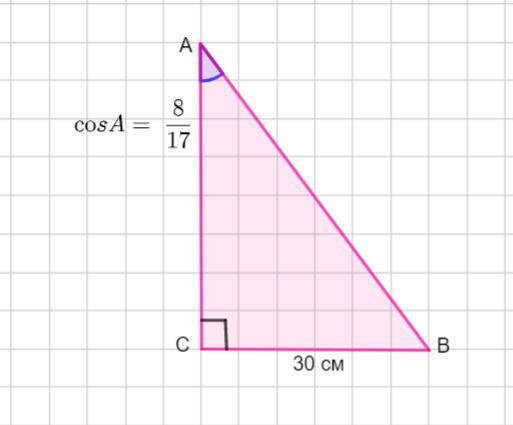
трикутник АВС прямокутний ВС=30 см, cos кута А = 8/17 ( дроб ), знайти периметр трикутника АВС!

Answer 1

Ответ:

Периметр треугольника равен 80 см.

Объяснение:

Треугольник АВС прямоугольный, ВС =30 см, соs А =8/17, найти периметр треугольника АВС

Пусть дан треугольник ΔАВ -прямоугольный, ∠С =90°. соs А =8/17, ВС =30 см.  Катет ВС противолежащий к углу ∠А, а косинус острого  угла прямоугольного треугольника - это отношение прилежащего катета к гипотенузе.

Поэтому найдем синус этого угла, используя основное тригонометрическое тождество

$sin^{2} A+cos^{2} A =1 ;\\sin^{2} A=1-cos^{2} A$

так как синус острого угла положителен, то

$sinA =\sqrt{1-cos^{2} A} ;\\sinA =\sqrt{1-\left(\dfrac{8}{17}\right)^{2} } =\sqrt{1-\dfrac{64}{289} } =\sqrt{\dfrac{289-64}{289} } =\sqrt{\dfrac{225}{289} } =\dfrac{15}{17} .$

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе

$sin A =\dfrac{BC }{AB } ;\\\\\dfrac{15 }{17 } =\dfrac{30 }{AB } ;\\\\AB =\dfrac{17\cdot 30}{15} =17\cdot 2 =34$

Значит, гипотенуза АВ равна 34 см

Найдем катет АС через косинус угла А

$cosA =\dfrac{AC}{AB} ;\\\\\dfrac{8}{17}=\dfrac{AC}{34};\\\\AC = \dfrac{8\cdot 34}{17} =8\cdot2=16$

Катет АС равен 16 см.

Периметр треугольника - это сумма длин всех сторон треугольника

P = AB +BC +AC

P= 34 +30 +16= 80 cм

#SPJ1