ДАМ 40 БАЛЛОВ!!!
УМОЛЯЮ ПОМОГИТЕ ПОЖАЛУЙСТА

Ответы
Відповідь:
Площадь вписаной окружности в четыре раза меньше площади описанной окружности.
Покрокове пояснення:
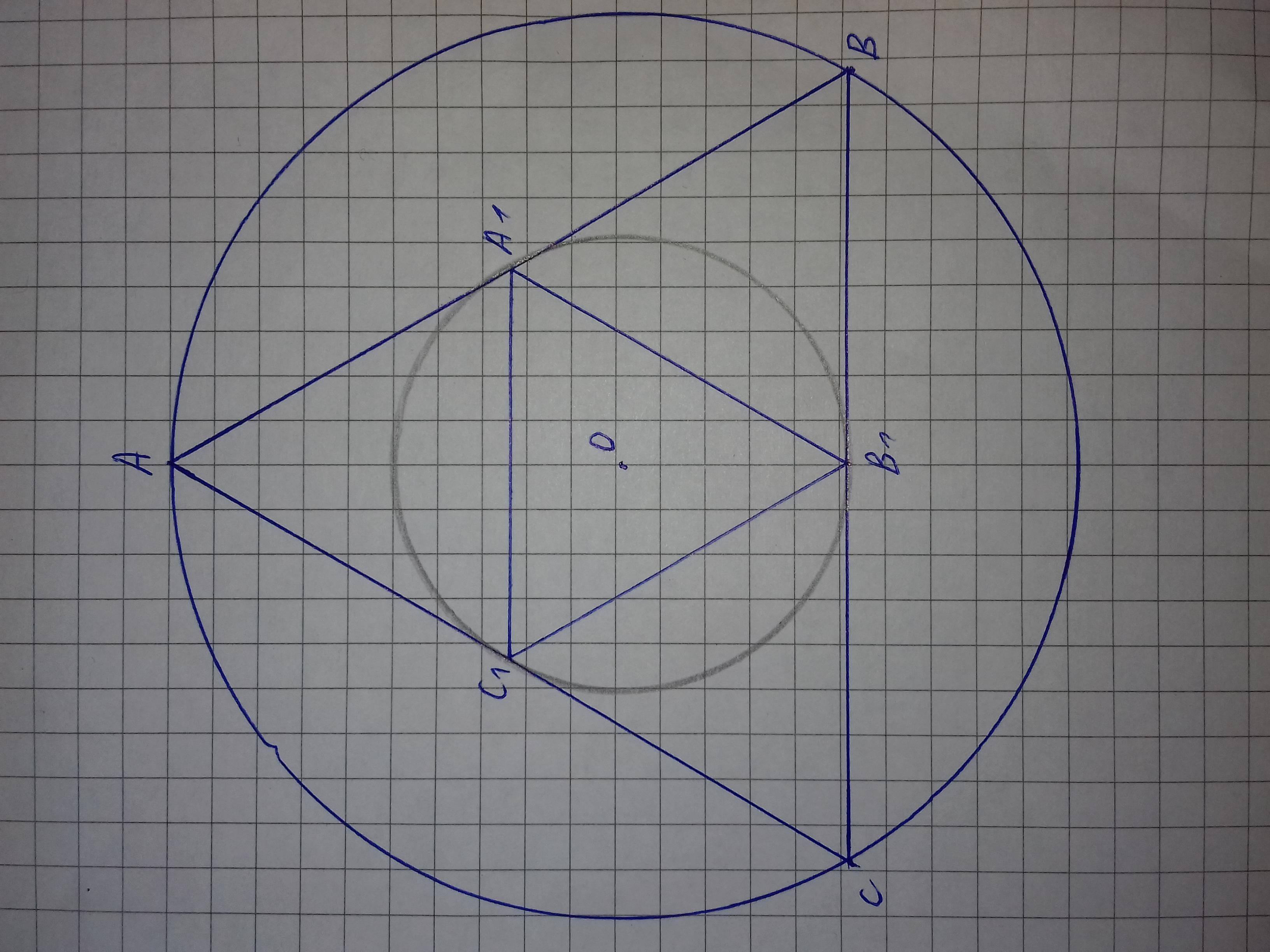
У нас есть равносторонний ∆АВС.
Около ∆АВС описана окружность радиусом R.
В ∆АВС вписана окружность радиусом r.
На серединах сторон ∆АВС ( АА1 = А1В, ВВ1 = В1С, СС1 = С1А ) построим ∆А1В1С1 ( точки А1, В1 и С1 - являются точками касания ∆АВС вписанной окружностью ).
Поскольку ∆АВС - равносторонний, то и четыре треугольника: ∆АА1С1, ∆А1ВВ1, ∆С1В1С и ∆А1В1С1 также равносторонние.
Так как точки А1, В1 и С1 - это середины сторон ∆АВС, то стороны четырех полученных треугольников в два раза меньше сторон ∆АВС.
Вывод треугольники АВС и А1В1С1 - подобны с коэффициентом подобия равным 2.
Отсюда получаем, что радиус описанной окружности R = ОА = ОВ = ОС в два раза больше радиуса висанной окружности r = ОА1 = ОВ1 = ОС1.
R = 2 × r
Запишем формулы для площадей
описанной окружности радиусом R:
S = π × R²
вписаной окружности радиусом r:
s = π × r²
В задаче спрашивалось: во сколько раз площадь вписаной окружности меньше площади описанной окружности?
Определим отношение s к S:
s / S = ( π × r² ) / ( π × R² ) = r² / R²
Подставим в уравнение R = 2 × r и получим:
s / S = r² / ( 2 × r )² = r² / 4r² = 1/4
Ответ: Площадь вписаной окружности в четыре раза меньше площади описанной окружности.
Для проверки можно воспользоваться формулами для вычисления радиусов вписаной и описанной окружностей:
R = a / √3
r = а / ( 2 × √3 )
а = АВ = ВС = СА - сторона треугольника.
Из формул видно, что радиус вписаной окружности в два раза меньше радиуса описанной окружности.
А поскольку площадь окружности пропорциональна радиусу в квадрате, то следовательно площадь вписаной окружности в четыре раза меньше площади описанной окружности.