Предмет: Алгебра,
автор: natiart06
с построением и объяснением пожалуйста
Приложения:

Ответы
Автор ответа:
1
Ответ: .
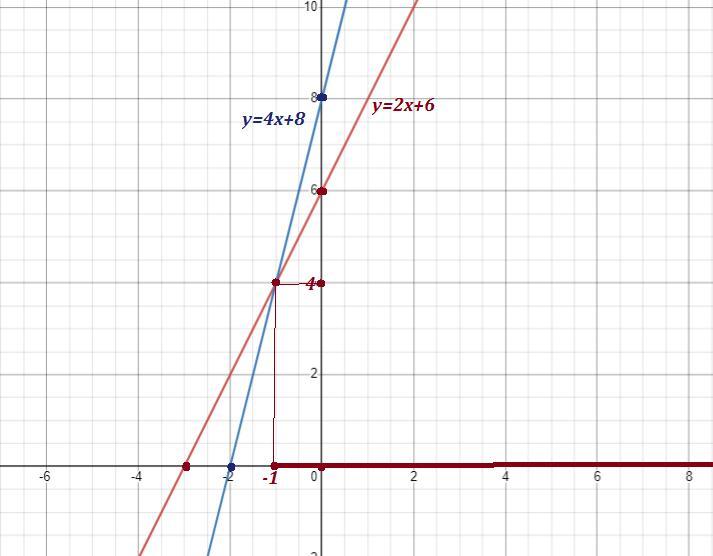
Найдём точку пересечения графиков функций .
Точка пересечения : .
Теперь найдём те значения переменной х , при которых , то
есть линия графика лежит ниже линии графика
.
Это будут .
Круглую скобку ставим потому, что знак неравенства строгий и значение х= -1 не входит в множество значений х , при которых выполняется заданное неравенство .
Приложения:
Похожие вопросы
Предмет: История,
автор: kovrnek
Предмет: Українська мова,
автор: vana67202
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: alyachebotareva04
Предмет: Физика,
автор: rex68431226