Question

30 БАЛЛОВ!! ПОМОГИТЕ ПОЖАЛУЙСТА!!! Куля радіуса 7√2 см дотикається до всіх сторін прямокутного трикутника з катетами 21 см і 28 см. Знайдіть відстань від центра кулі до площини трикутника.
Шар радиуса 7√2 см касается всех сторон прямоугольного треугольника с катетами 21 см и 28 см. Найдите расстояние от центра шара до плоскости треугольника.​

Answer 1

надо найти радиус вписанной окружности в треугольник

S=pr

r=S/p

гипотенуза c^2=21^2+28^2=35^2

p=(21+28+35)/2=42

S=28*21/2=294

r=294/42=7

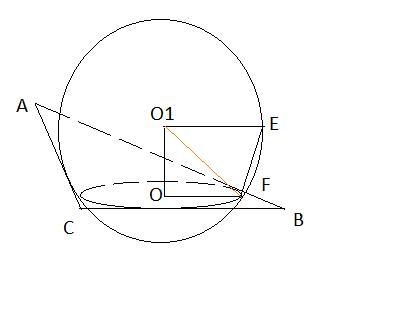
На рисунке r=OF=7; R=O1E=7√2

O1EFO-прямоугольная трапеция, найти ОО1=?

Соединю О1 и F, получу ΔO1OF- прямоугольный

O1F=R=7√2, тогда по т Пифагора

OO1^2=O1F^2-OF^2=(7√2)^2-7^2=98-49=49

OO1=7-ответ

(расстояние от центра шара до плоскости треугольника-это длина перпендикуляра из центра шара до центра вписанной окружности в треугольник)