Доведіть тотожність sin(a+B) - sin(a-3) cos(a+B) + cos(a-B) =tgB.
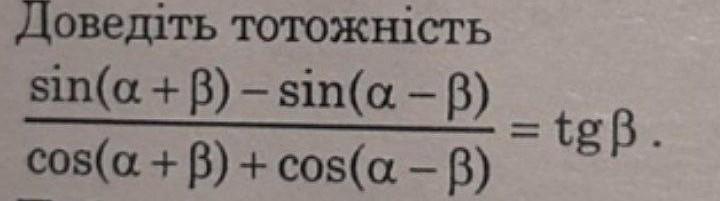
Ответы
Ответ:
Для доведення цієї тотожності ми скористаємося наступними тригонометричними формулами:
sin(x+y) = sin(x)cos(y) + cos(x)sin(y)cos(x+y) = cos(x)cos(y) - sin(x)sin(y)tan(x) = sin(x) / cos(x)
Застосуємо першу формулу до sin(a+B):
sin(a+B) = sin(a)cos(B) + cos(a)sin(B)
Застосуємо другу формулу до cos(a-B):
cos(a-B) = cos(a)cos(B) + sin(a)sin(B)
Тепер, застосовуючи ці результати, ми можемо записати:
sin(a+B) - sin(a-3)cos(a+B) + cos(a-B) =
(sin(a)cos(B) + cos(a)sin(B)) - sin(a-3)cos(a+B) + (cos(a)cos(B) + sin(a)sin(B))
= cos(a)cos(B) + sin(a)sin(B) - sin(a-3)cos(a+B) + cos(a)cos(B) + sin(a)sin(B)
= 2cos(a)cos(B) - sin(a-3)cos(a+B)
Тепер ми можемо використати третю формулу, щоб виразити tg(B) через sin(B) і cos(B):
tg(B) = sin(B) / cos(B)
Отже, щоб довести тотожність, ми повинні показати, що:
2cos(a)cos(B) - sin(a-3)cos(a+B) = sin(B) / cos(B)
Ми можемо перетворити праву частину виразу, використовуючи третю формулу, тобто:
sin(B) / cos(B) = tg(B)
Тепер, підставляючи tg(B) в останнє рівняння, ми отримуємо:
2cos(a)cos(B) - sin(a-3)cos(a+B) = tg(B)
Отже, ми довели задану тотожність.
Ответ:
Доказано требуемое.
Объяснение:
Мы воспользовались формулами