Question

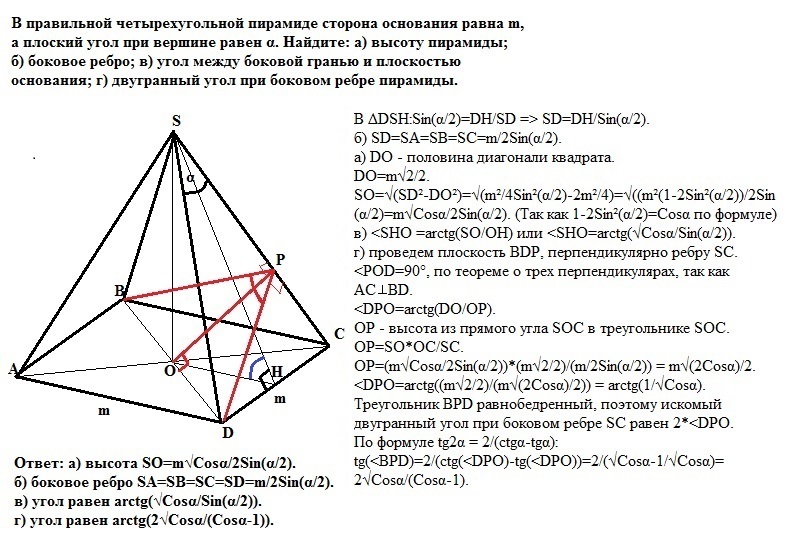
В правильной четырехугольной пирамиде сторона основания равна m, а плоский угол при вершине равен α. Найдите: а) высоту пирамиды; б) боковое ребро; в) угол Между боковой гранью и плоскостью основания; г) двугранный угол при боковом ребре пирамиды
ОБЯЗАТЕЛЬНО РИСУНОК

Answer 1

В ΔDSH:Sin(α/2)=DH/SD => SD=DH/Sin(α/2).
б) SD=SA=SB=SC=m/(2Sin(α/2)).
а) DO - половина диагонали квадрата.
DO=m√2/2.
SO=√(SD²-DO²)=√(m²/4Sin²(α/2)-2m²/4)=√((m²(1-2Sin²(α/2))/2Sin(α/2)=
m√Cosα/2Sin(α/2).  (Так как 1-2Sin²(α/2)=Cosα по формуле).
в) <SHO =arctg(SO/OH) или <SHO=arctg(√Cosα/Sin(α/2)).
г) проведем плоскость ВDP, перпендикулярно ребру SC.
<POD=90°, по теореме о трех перпендикулярах, так как АС⊥BD.
<DPO=arctg(DO/OP).
ОР - высота из прямого угла SOC в треугольнике SOC.
ОР=SO*OC/SC.
OP=(m√Cosα/2Sin(α/2))*(m√2/2)/(m/2Sin(α/2)) = m√(2Cosα)/2.
<DPO=arctg((m√2/2)/(m√(2Cosα)/2)) = arctg(1/√Cosα).
Треугольник ВPD равнобедренный, поэтому искомый двугранный угол при боковом ребре SС равен 2*<DPO.
По формуле tg2α = 2/(ctgα-tgα):
tg(<BPD)=2/(ctg(<DPO)-tg(<DPO))=2/(√Cosα-1/√Cosα)=2√Cosα/(Cosα-1).

Ответ: а) высота SO=m√Cosα/(2Sin(α/2)).
б) боковое ребро SA=SB=SC=SD=m/2Sin(α/2).
в) угол равен arctg(√Cosα/Sin(α/2)).
г) угол равен arctg(2√Cosα/(Cosα-1)).