Предмет: Алгебра,
автор: melissashykalova
ДАЮ 50 БАЛОВ!!! ПРОШУ ПОМОГИТЕ!!!!
Приложения:
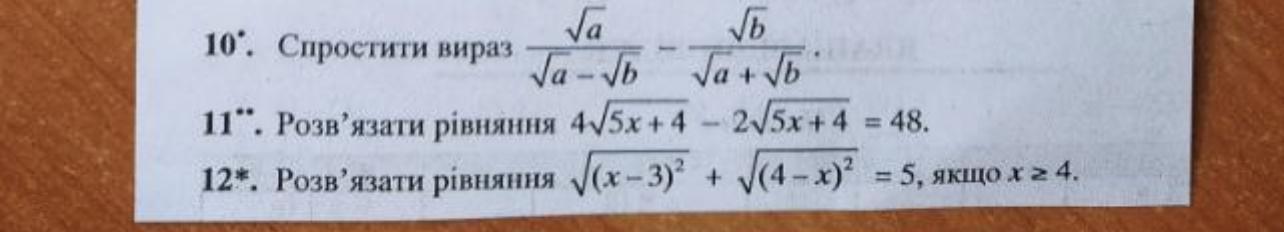
Ответы
Автор ответа:
1
Ответ:
10) Применяем формулу разности квадратов .
11) Иррациональное уравнение .
12) Если , то
, тогда
,
a . Учтём, что
.
Похожие вопросы
Предмет: Математика,
автор: imanovazamat028
Предмет: Английский язык,
автор: Аноним
Предмет: Геометрия,
автор: cvb115
Предмет: История,
автор: Vyatkina17
Предмет: Алгебра,
автор: rabiasabyrzhanovna