1). Знайди значення f(-4), f(-0,3), f(1,9), f(3), f(-1), f(2).
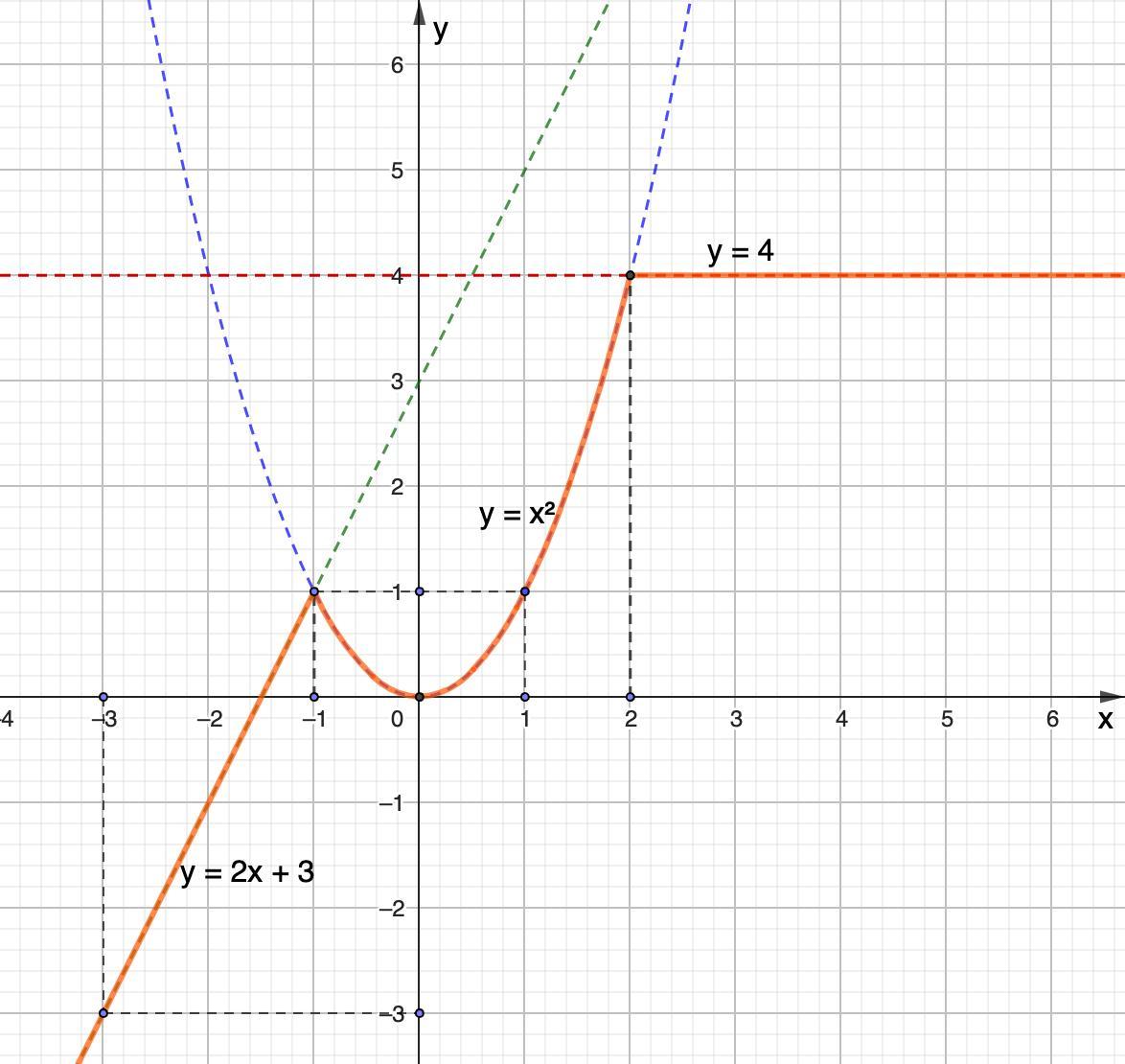
2). Побудуй графік даної функції.
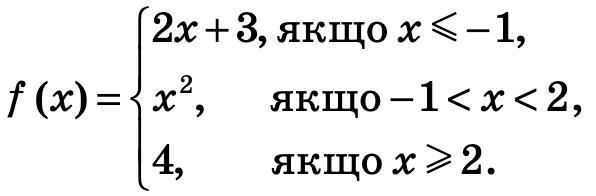
Ответы
Ответ:
1) f(-4) = -5, f(-0,3) = 0,09, f(1,9) = 3, 61, f(3) = 4, f (-1) = 1, f(2) = 4
2) График построен.
Объяснение:
1). Найди значения f(-4), f(-0,3), f(1,9), f(3), f (-1), f(2).
2). Построй график данной функции.
Имеем кусочно - заданную функцию.
По условию задано три участка.
1) Найдем значения функций при заданных аргумента. Для этого определим, какому участку принадлежит аргумент.
f(-4) ⇒ x ≤ -1
f(-4) = 2 · (-4) + 3 = -8 + 3 = -5
f(-0,3) ⇒ -1 < x < 2
f(-0,3) = (-0,3)² = 0,09
f(1,9) ⇒ -1 < x < 2
f(1,9) = (1,9)² = 3,61
f(3) ⇒ x ≥ 2
f(3) = 4
f(-1) ⇒ x ≤ -1
f(-1) = 2 · (-1) + 3 = 1
f(2) ⇒ x ≥ 2
f(2) = 4
2). Построим график данной функции.
Нужно каждый кусочек функции построить на выделенном для него участке.
1. f(x) = 2x + 3, если х ≤ -1
- линейная функция, график - прямая.
Для построения достаточно двух точек:
Эта часть графика расположена левее точки х = -1, причем эта точка входит в данный кусочек графика.
Строим график.
2. f(x) = x², если -1 < x < 2
- квадратичная функция, график - парабола, ветви вверх.
Эта часть графика расположен на участке -1 < x < 2.
Строим график.
3. f(x) = 4, если х ≥ 2.
- прямая параллельная оси Ох с ординатой у = 4.
График кусочно - заданной функции построен.
#SPJ1