Помогите П Ж, ничего не понимаю

Ответы
Ответ:
1. Проекции катетов на гипотенузу равны 4 ед. и 12 ед.
2. Площадь треугольника АВС равна 600 см².
3. Катет равен 31,2 см; гипотенуза равна 33,8 см.
Объяснение:
Задача 1.
Катает прямоугольного треугольника 8, гипотенуза 16. Найдите проекции катетов на гипотенузу.
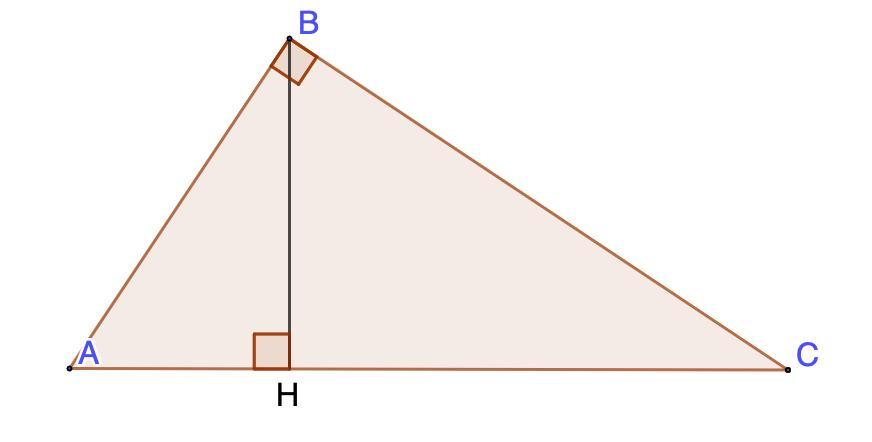
Дано: ΔАВС - прямоугольный.
АВ = 8 - катет; АС = 16 - гипотенуза.
ВН - высота.
Найти: АН и НС.
Решение:
В данных задачах воспользуемся метрическими соотношения в прямоугольном треугольнике:
- Квадрат высоты, опущенной из вершины прямого угла на гипотенузу, равен произведению проекций катетов на гипотенузу. А квадрат каждого катета равен произведению проекции данного катета на гипотенузу и самой гипотенузы.
⇒ АВ² = АН · АС
64 = АН · 16 ⇒ АН = 4
Тогда НС = 16 - 4 = 12
Проекции катетов на гипотенузу равны 4 ед. и 12 ед.
Задача 2
Проекции катетов на гипотенузу 18 см и 32 см. Найдите площадь прямоугольного треугольника и его катеты.
Дано: ΔАВС - прямоугольный;
ВН - высота;
АН = 18 см; НС = 32 см - проекции катетов на гипотенузу.
Найти: S(ABC)
Решение:
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.
S(ABC) = 1/2 · AC ·BH
AC - AH + HC = 18 + 32 = 50 (см)
ВН² = АН · НС = 18 · 32 = 576 ⇒ ВН = √576 = 24 (см)
S(ABC) = 1/2 · 50 · 24 = 600 (см²)
Площадь треугольника АВС равна 600 см².
Задача 3.
Найдите гипотенузу и катет прямоугольного треугольника, если высота, проведённая к гипотенуза 12 см, а другой катет равен 13 см.
Дано: ΔАВС - прямоугольный;
ВН = 12 см - высота;
АВ = 13 см;
Найти: ВС; АС.
Решение:
Рассмотрим ΔАВН - прямоугольный.
По теореме Пифагора найдем АН:
АН² = АВ² - ВН² = 169 - 144 = 25 ⇒ АН = √25 = 5 (см)
Найдем гипотенузу АС.
АВ² = АН · АС
169 = 5 · АС
АС = 169/5 = 33,8 (см)
Рассмотрим ΔАВС - прямоугольный.
По теореме Пифагора найдем катет ВС:
ВС² = АС² - АВ² = 1142,44 - 169 = 973,44 ⇒ ВС = √973,44 = 31,2 (см)
Катет равен 31,2 см; гипотенуза равна 33,8 см.