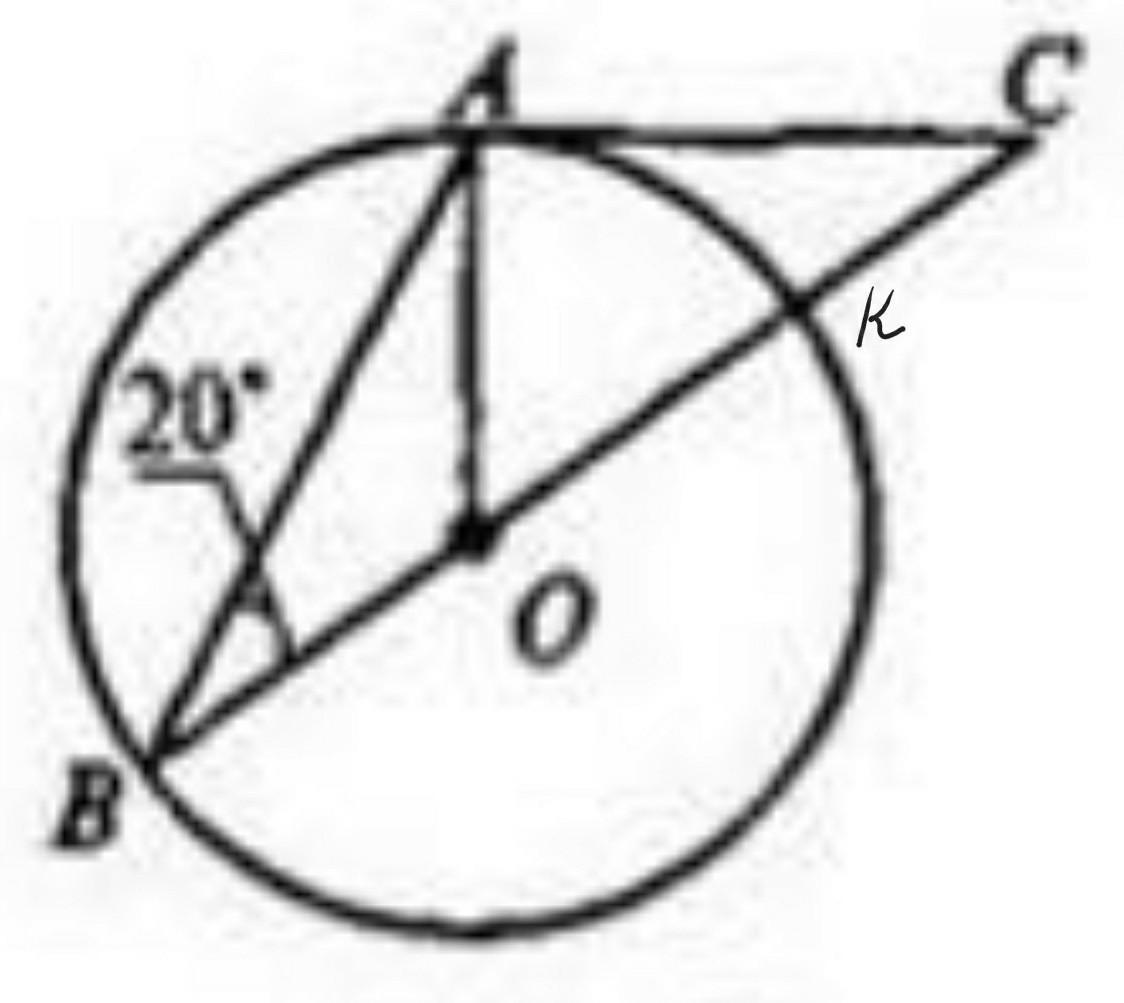
Дано: AC-дотична до кола. Знайти кут АСВ. ( даю все баллы, срочно очень)
Ответы
ОА і ОВ—радіуси кола, відповідно вони рівні між собою, тоді кути ОВА і ОАВ також рівні. тоді кут АОВ =180-20-20=140°
Кут ОАС—прямокутний =90°
Кут ВОА і кут АОС суміжні, тому АОС=180-140=40°
і так ОАС=90°, АОС=40°
АСО=180-90-40=50°
Ответ:
∠ACB=50°
Объяснение:
Дано: AC-дотична до кола. Знайти кут АСВ.
1 спосіб
- Центральним кутом називають кут з вершиною у центрі кола
- Вписаним кутом називають кут, вершина якого належить колу, а сторони перетинають його.
- Вписаний кут дорівнює половині центрального кута, що спирається на ту ж дугу.
- Дототична до кола перпендикулярна до радіуса, проведеного в точку дотику.
Розв'язання
∠AOC - центральний кут, спирається на дугу ◡AK.
∠ABС - вписаний кут, спирається на дугу ◡AK. За умовою ∠ABС=20°
∠ABС=½•∠AOC ⇒
∠AOC=2•∠ABС=2•20°=40°
АС - дотична до кола, АО - радіус кола. ⇒ AC⟂AO.
△ACO - прямокутний, ∠ОАС=90°
За теоремою про суму кутів прямокутного трикутника знайдемо кут АСВ.
∠АСВ=90°-∠АОС=90°-40°=50°
Відповідь: 50°.
2 спосіб
1) OA=OB - как радіуси кола, тому △АОВ - рівнобедрений з основою АВ.
∠ОАВ=∠ОВА - як кути при основі рівнобедреного трикутника.
Тоді, за теоремою про суму кутів трикутника знайдемо кут AOB:
∠AOB=180°-20°-20°=140°
2) АС - дотична до кола, АО - радіус кола. ⇒ AC⟂AO.
△ACO - прямокутний, ∠ОАС=90°.
∠AOB - зовнішній кут △ACO, він дорівнює сумі двох внутрішніх кутів, не суміжних з ним:
∠AOB=∠OAC+∠ACO
140°=90°+∠AOC
∠AOC=140°-90°=50°
Відповідь: 50°.