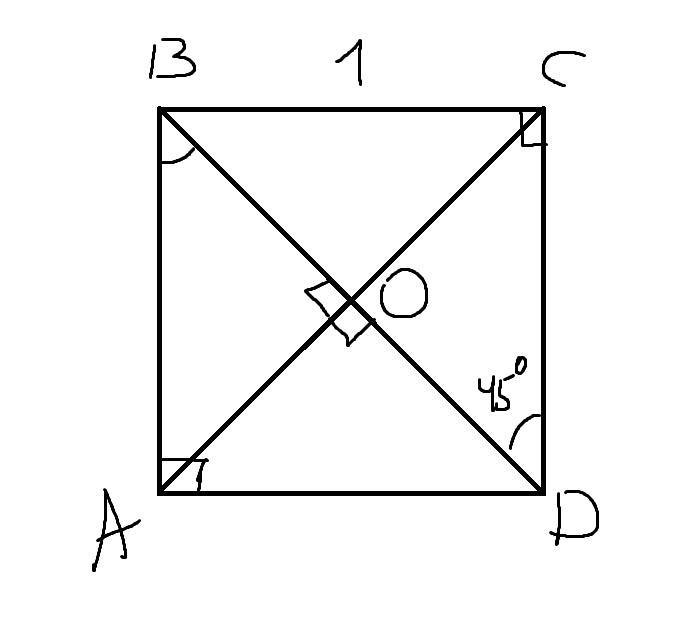
у квадраті АВСD сторона дорівнює 1. Діагоналі перетинаються в точці О.Знайдіть скалярний добуток векторів:а)АО і ВD; б) СО і CD; в)АВ і DB.Допоможіть будь ласка.до 15.00
Ответы
Відповідь:
Пояснення:
У квадраті ABCD зі стороною 1 діагоналі AC і BD перетинаються в точці O. Знайдемо скалярний добуток цих векторів:
a) AO і BD: Оскільки AO - половина діагоналі AC, а BD - діагональ квадрата, ми можемо використати теорему Піфагора, щоб знайти їх довжини: |AO = AC = 2 = sqrt(1² + 1²)/2 = sqrt(2)/2 BD = AC = sqrt(2)
Кут між векторами AO і BD дорівнює 45 градусів, оскільки діагоналі квадрата перетинаються під прямим кутом, а AO дорівнює половині діагоналі AC. Тому AO - BD = |AO||BD|cos(45°) = (sqrt(2)/2)(sqrt(2))cos(45°) = 1
б) CO і CD: Оскільки CO - половина діагоналі AC, а CD - сторона квадрата довжиною 1: |CO| = |AC|/2 = sqrt(2)/2 |CD| = 1
Кут між векторами CO і CD також дорівнює 45 градусів, оскільки діагоналі квадрата перетинаються під прямим кутом, а CO дорівнює половині діагоналі AC. Тому CO - CD = |CO||CD|cos(45°) = (sqrt(2)/2)(1)cos(45°) = sqrt(2)/2
c) AB і DB: Оскільки AB і DB - сторони квадрата довжиною 1, то |AB|= |DB|= 1
Кут між векторами AB і DB також дорівнює 45 градусів, оскільки вони є сторонами, прилеглими до однієї діагоналі. Тому AB - DB= |AB||DB|cos(45°)= (1)(1)cos(45°)= sqrt(2)/2