Question

ДАЮ 100 БАЛЛІВ!!!!!!!!!!

Answer 1

Исследуйте функции и постройте их график :

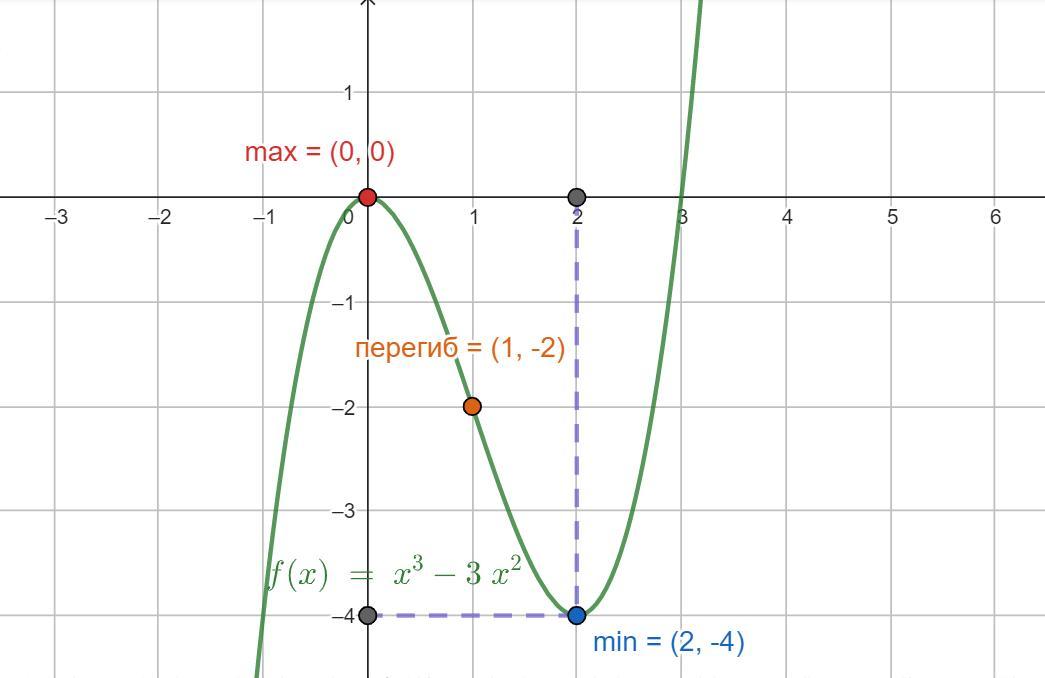
a) y = x³ - 3x²

1. Область определения :

$D(y)= \mathbb R$

2. Четность нечетность :

$f(-x)= -x^3 -3x^2 \neq \pm f(x) \Rightarrow$  не является ни четной ,  ни нечетной

3. Пересечение с осями координат :

I)

Ox ⇒ y = 0

x³ - 3x² = 0

x²(x-3) = 0

x = 0 ;  x = 3

II)

Oy ⇒ x = 0

y = 0³ - 3·0² = 0

4. Непрерывность :

Функция непрерывна , асимптот  нет

5. Возрастание убывание , экстремумы :

y'= (x³ - 3x²)' =  3x² - 6x = 3x(x-2)

$\setlength{\unitlength}{23mm}\begin{picture}(1,1) \linethickness{0.2mm} \put(.96,-0.3) {\sf 0} \put(.2 ,0.1){ \Large \text{ +} } \put(.17 ,-0.2){ \Large \nearrow } \put(1.3 ,0.1){ \LARGE ---} \put(1.3 ,-0.2){ \Large \searrow } \put(2.25 ,0.1){ \Large \text{ +} } \put(1,0){\circle*{0.055}} \put(2.25 ,-0.2){ \Large \nearrow } \put(2.02,-0.3) {\sf 2}\put(2.05,0){\circle*{0.055}} \put(1,0.3) \ \put(0,0){\vector (1,0){3}} \end{picture}$

$\Large \boldsymbol{ \nearrow }$ Возрастает когда $x\in( -\infty ~ ; ~ 0~ ] ~; ~ [~2~ ; ~ \infty ~)$

$\Large \boldsymbol{ \searrow }$  Убывает когда $x \in [~ 0 ~ ; ~ 2~]$

Если производная меняет знак c «+» на «-» , то в данной точке будет максимум , если c «-» на «+», то минимум .

Следовательно:
$x _{ max} = 0 ~ ;~ y _{max} = 0^3 - 3\cdot 0^2 = 0 \\\\ x_{min}= 2 ~ ; ~ y_{min }= 8 -12 = - 4$

6. Выпуклость вогнутость :

Находим вторую производную

(y')'=(3x² - 6x)' = 6x - 6

Приравниваем к нулю :
6x - 6= 0

x = 1

$\setlength{\unitlength}{23mm}\begin{picture}(1,1) \linethickness{0.2mm} \put(1.45,-0.3) {\sf 1} \put(.5 ,0.1){ \LARGE \text{ ---} } \put(2.1 ,0.1){ \Large \text{ +} } \put(1.5,0){\circle*{0.055}} \put(0,0){\vector (1,0){3}} \end{picture}$

Если     « + »  , то функция  вогнута

Если     «—»  , то функция выпукла

Таким образом :

Если $x \in [~ 1 ~ ; ~ \infty )$   функция вогнута

Если $x \in (- \infty ~ ; ~ 1]$  функция выпукла

7.График в приложенном файле

б) $y = \dfrac{2}{x} - \dfrac{x}{2}$

1. Область определения :

$D(y)= (-\infty ~ ;~ 0 ) \cup (0 ~ ; ~ \infty )$

2.Точка разрыва

x = 0

$\displaystyle \lim_{n \to 0-0}\bigg (\frac{2}{x}- \frac{x}{2} \bigg ) = \lim_{n \to 0-0}\frac{4-x^2}{2x} = - \infty$

$\displaystyle \lim_{n \to 0+0}\dfrac{4-x^2}{2x} = \infty$

x = 0  — точка разрыва 2-го рода
3. Четность нечетность :

$f(-x)= -\dfrac{2}{x}+\dfrac{x}{2} = - f(x) \Rightarrow$  является ни четной

4. Пересечение с осями координат :

Ox ⇒ y = 0

$\dfrac{2}{x}- \dfrac{x}{2} = 0 \\\\\\ \dfrac{4-x^2}{2x}= 0 \\\\ x= 2 ~ ; ~ x = -2$

5.Непрерывность :

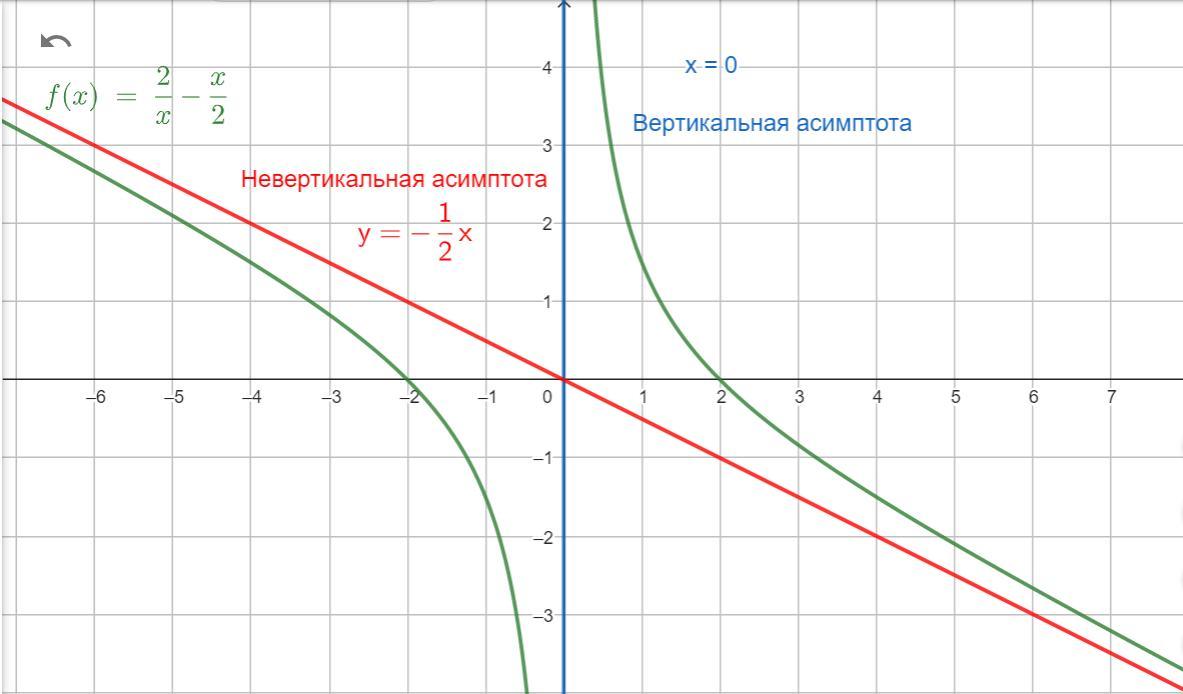
x = 0 — вертикальная асимптота

Находим невертикальную асимптоту

y = kx + b

$\displaystyle k = \lim_{x \to \pm\infty} \frac{f(x)}{x} ~ ; ~b = \lim_{n \to \pm\infty}\big(f(x)-kx \big )$

$\displaystyle k = \lim_{x \to \pm\infty} \frac{4-x^2}{2x^2} = \lim_{x \to \pm\infty} \frac{\dfrac{4}{x^2} -\dfrac{x^2}{x^2} }{2\cdot \dfrac{x^2}{x^2} } = \lim_{x \to \pm\infty} \frac{-1+ \dfrac{4}{x^2} }{2} = - \frac{1}{2}$

$\displaystyle b = \lim_{n \to \pm\infty}\Bigg (\frac{4-x^2}{2x}- \bigg(- \frac{x}{2} \bigg) \Bigg ) = \lim_{n \to \pm\infty} \frac{4}{2x}= 0$

$y =-\dfrac{1}{2}x$  — невертикальная асимптота

6. Возрастание убывание , экстремумы :

$y '= \displaystyle \bigg ( \frac{2}{x}-\frac{x}{2} \bigg ) ' = -\frac{2}{x^2} - \frac{1}{2} = -\frac{4+x^2}{2x^2}$

$\setlength{\unitlength}{23mm}\begin{picture}(1,1) \linethickness{0.2mm} \put(.6,-0.2){ \Large \searrow } \put(2.15 ,-0.2){ \Large \searrow } \put(1.45,-0.3) {\sf 0} \put(.5 ,0.1){ \LARGE \text{ ---} } \put(2.1 ,0.1){ \LARGE \text{--- } } \put(1.5,0){\circle{0.055}} \put(0,0){\vector (1,0){3}} \end{picture}$

Экстремумов нет ,  функция убывает на всей области определения

$\Large \boldsymbol{ \searrow }$   $x\in( -\infty ~ ; ~ 0~ ) ~; ~ (~0~ ; ~ \infty ~)$

7. Выпуклость вогнутость :

Находим вторую производную

$(y ')'= \displaystyle \bigg ( -\frac{2}{x^2} - \frac{1}{2} \bigg )' = -2\cdot (-2)\frac{1}{x^3}= \frac{4}{x^3}$

x = 0 — точка разрыва

$\setlength{\unitlength}{23mm}\begin{picture}(1,1) \linethickness{0.2mm} \put(1.45,-0.3) {\sf 0} \put(.5 ,0.1){ \LARGE \text{ ---} } \put(2.1 ,0.1){ \Large \text{ +} } \put(1.5,0){\circle{0.055}} \put(0,0){\vector (1,0){3}} \end{picture}$

Если $x \in (~ 0 ~ ; ~ \infty )$   функция вогнута

Если $x \in (- \infty ~ ; ~ 0)$  функция выпукла

8.График в приложенном файле