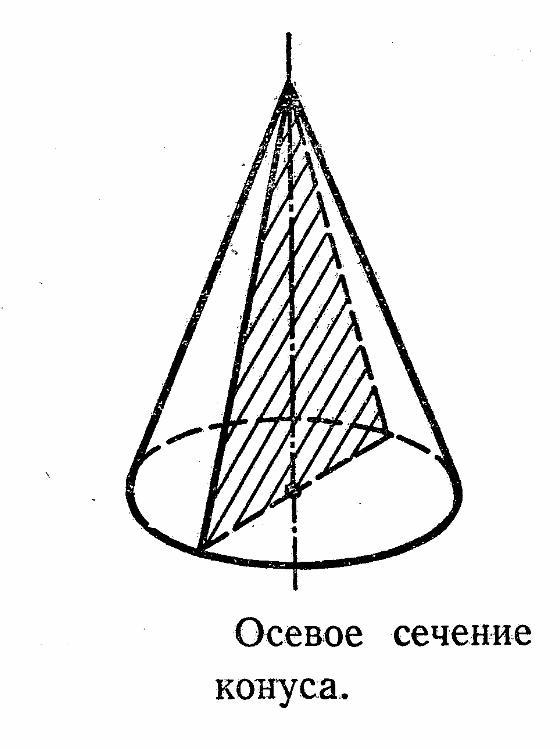
осьовим перерізом конуса є правильний трикутник сторона якого дорівнює 4√3см.обчислити об'єм конуса
РЕШИТЬ С РИСУНКОМ ДАЮ 70 БАЛЛОВ
Ответы
Ответ:
Объем правильного конуса можно вычислить по формуле:
V = (1/3) * π * r^2 * h,
где r - радиус основания конуса, h - высота конуса.
В данном случае основание конуса является правильным треугольником со стороной 4√3 см. Таким образом, радиус основания равен половине диагонали, которая находится по теореме Пифагора:
r = a/2√3 = (4√3)/2√3 = 2 см.
Высоту конуса можно найти, решив уравнение прямой треугольной пирамиды, находящейся внутри конуса. Так как у этой пирамиды основание находится внутри основания конуса, а вершина пирамиды совпадает с вершиной конуса, то ее высота также является высотой конуса. Значит,
h^2 = a^2 − r^2 = (4√3)^2 − 2^2 = 48 − 4 = 44.
h = 2√11 см.
Теперь можем подставить значения радиуса и высоты в формулу для объема:
V = (1/3) * π * r^2 * h = (1/3) * π * 2^2 * 2√11 = (4/3) * π * √11 ≈ 14.57 см^3.
Ответ: объем конуса примерно равен 14.57 см^3.