Побудуй графік нерівності
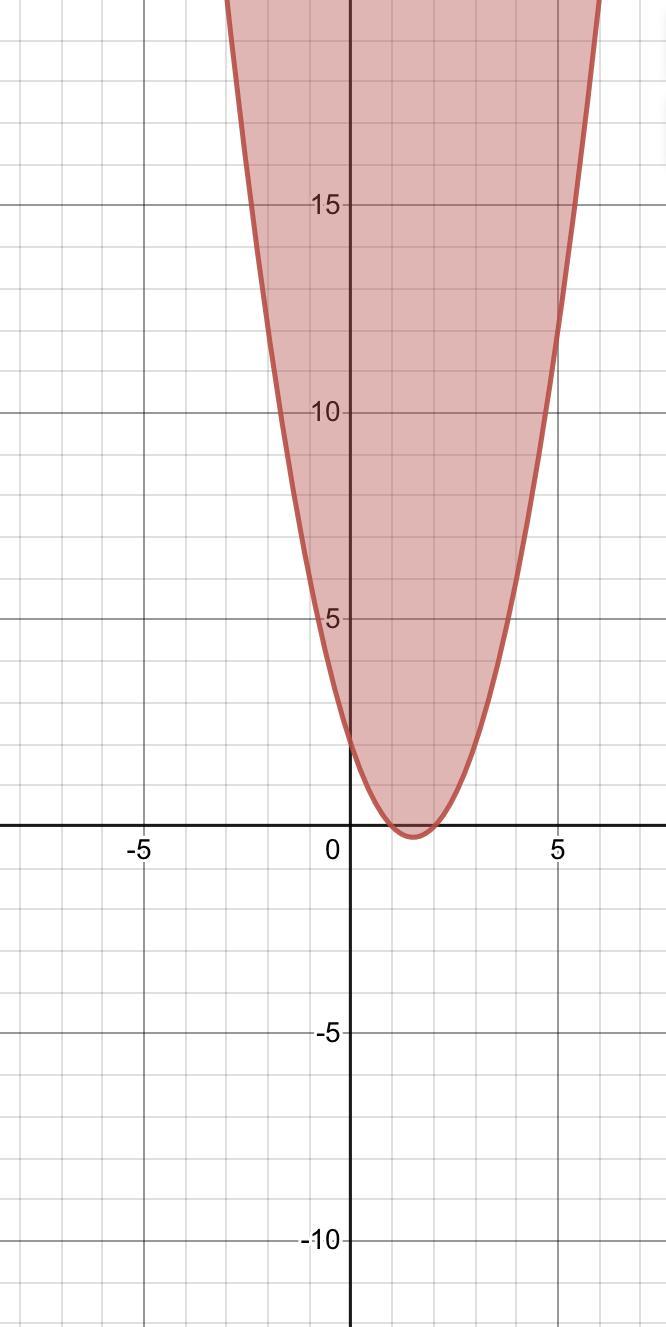
1)y ≥ x² - 3x + 2
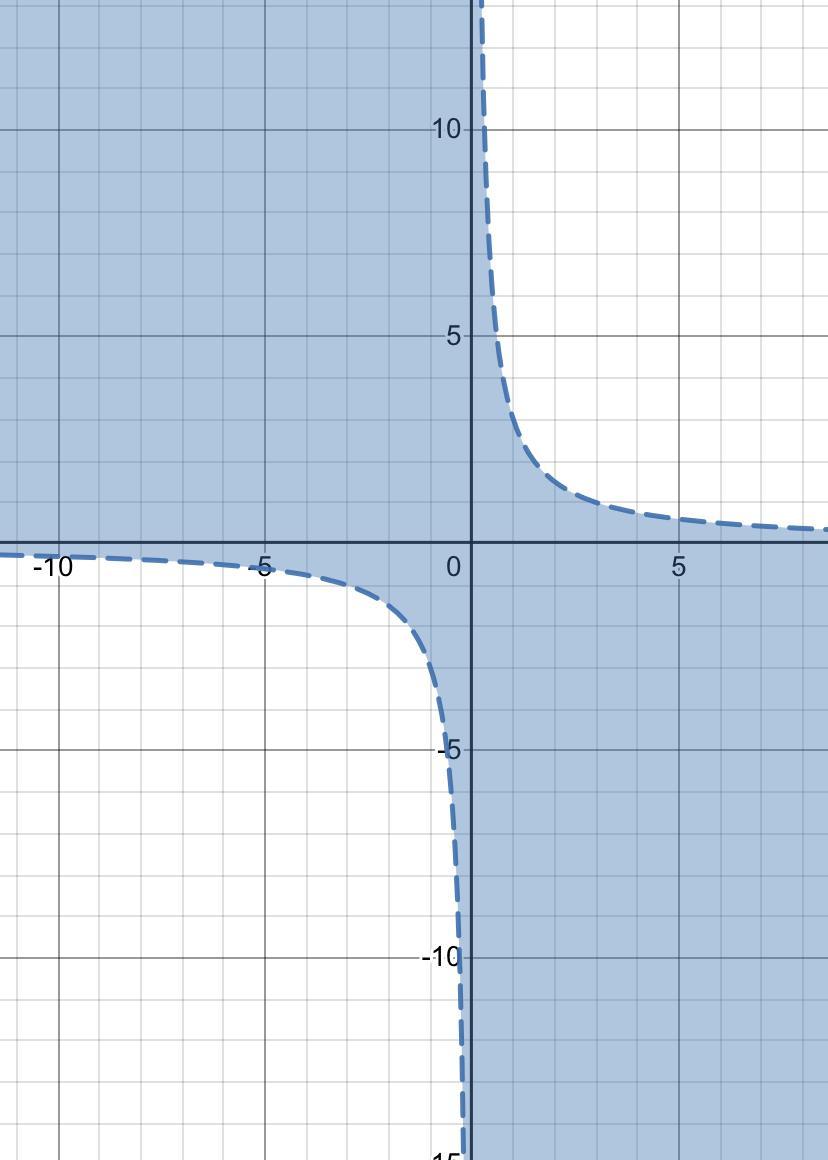
2)xy<3
Ответы
y ≥ x² - 3x + 2
Рожева парабола
xy<3
Блакитна
Пояснення:
1. Щоб намалювати графік нерівності y ≥ x² - 3x + 2, спочатку знайдемо вершину параболи, яка відповідає виразу x² - 3x + 2.
Вершина параболи має координати:
x = -(-3) / (2*1) = 3/2y = (3/2)² - 3(3/2) + 2 = -1/4
Тож, вершина параболи має координати (3/2, -1/4).
Тепер, можемо побудувати графік параболи, яка відповідає виразу x² - 3x + 2 та перевірити, які значення y знаходяться вище параболи. Ці значення задовольняють нерівність y ≥ x² - 3x + 2.
Для перевірки, чи задовольняє точка підставлення в нерівність, достатньо перевірити, чи знаходиться точка вище параболи, тобто чи виконується умова y ≥ x² - 3x + 2.
Наприклад, якщо ми хочемо перевірити, чи задовольняє точка (1, 1) нерівність, ми підставляємо значення x і y в нерівність та отримуємо:
1 ≥ 1² - 3(1) + 21 ≥ 0
Умова виконується, тому точка (1, 1) задовольняє дану нерівність.
2. Щоб побудувати графік нерівності xy<3, спочатку треба побудувати графік функції y = 3/x. Ця функція є гіперболою з вертикальною та горизонтальною асимптотами.