Предмет: Математика,
автор: MaybelMaybel
Терміново! Допоможіть розв'ятати задачі з вищої математики (на фото):
Приложения:

Ответы
Автор ответа:
1
Відповідь:
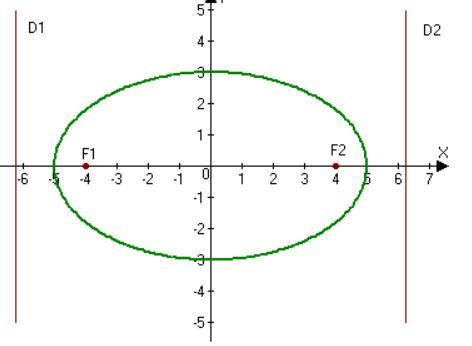
Задача 1. Рівняння лінії.
Канонічне рівняння для знаходження довжини осей:
A=5, B= 3
Координати фокусів :
Точки F1(−c,0) ,F2(c,0)- фокуси,
де c=
c=
Отже, F1(−4,0),F2(4,0).
Ексцентриситет:
e==0,8
Рівняння дисетрис (для еліпса):
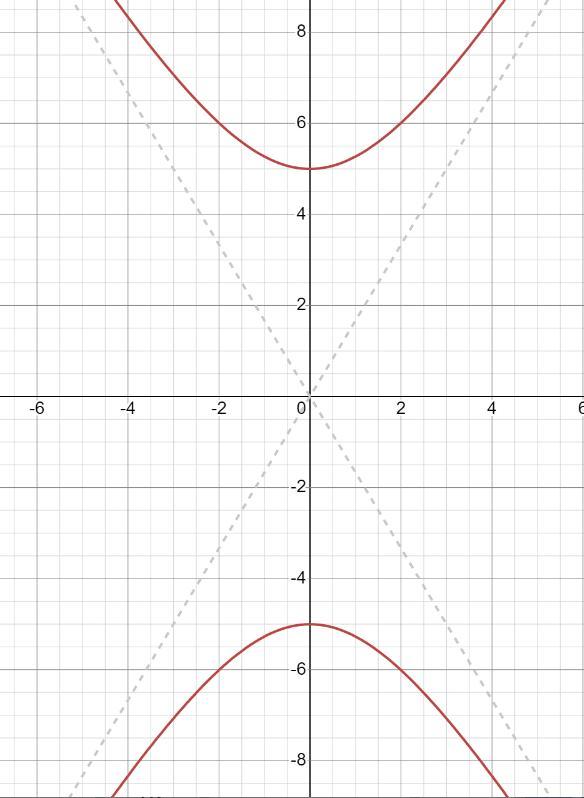
Рівняння асимптот:
y=+-
y=-
y=
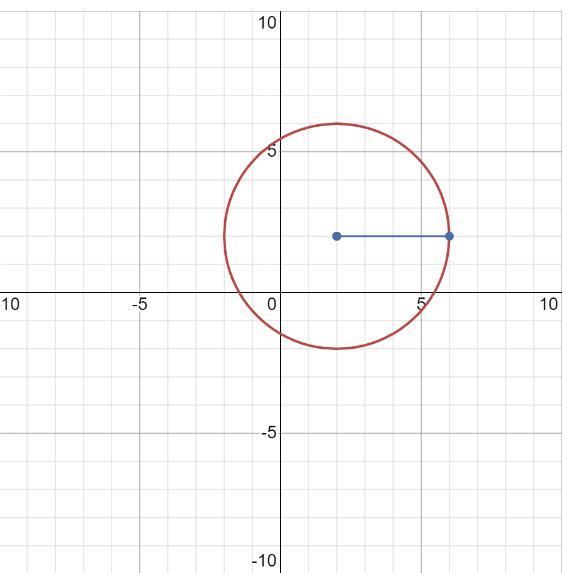
Задача 2.
Формула кола:
(
r-радіус кола
h-зсув по осі X від початку координат, а
k- зсув по осі Y від початку координат.
Координати центра кола знаходяться в точках (h,k)=(2;2)
Радіус кола = 4
Приложения:
MaybelMaybel:
До якого завдання відноситься 2 малюнок?
вибач, забула відмитити. 1 мал. до задачі 1
2 мал. до рівняння асимптот . 3 мал. задача 2
2 мал. до рівняння асимптот . 3 мал. задача 2
Тепер зрозуміло, дуже дякую!
Похожие вопросы
Предмет: История,
автор: mariaskabarna0
Предмет: Английский язык,
автор: r8009496
Предмет: Алгебра,
автор: aoxzz00228
Предмет: Литература,
автор: elza005