Ришите уравнение

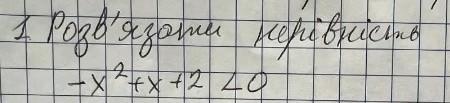
Ответы
Для решения данного неравенства нам нужно найти корни квадратного уравнения, полученного из исходного путем замены знака неравенства на знак равенства:
-x^2 + x + 2 = 0
Решим это квадратное уравнение, используя формулу корней:
x = (-b ± sqrt(b^2 - 4ac)) / 2a
где a = -1, b = 1 и c = 2. Подставляем значения:
x = (-1 ± sqrt(1 - 4(-1)(2))) / 2(-1)
x = (-1 ± sqrt(1 + 8)) / (-2)
x = (-1 ± sqrt(9)) / (-2)
x = (-1 + 3) / (-2) или x = (-1 - 3) / (-2)
x = -1/2 или x = 2
Таким образом, корни квадратного уравнения -1/2 и 2 являются точками пересечения графика квадратной функции с осью абсцисс. Неравенство -x^2 + x + 2 < 0 выполнено на интервалах (-бесконечность, -1/2) и (2, +бесконечность).
Итак, решение неравенства -x^2 + x + 2 < 0 может быть записано в виде:
x ∈ (-∞, -1/2) ∪ (2, +∞)
Объяснение:
-х²+х+2<0
х²-х-2>0
D=(-1)²-4•1•(-2)=9
x1=(1-3)/2= -1
x2=(1+3)/2=2
+ - +
———o————o——
-1 2
x∈(-∞;-1)⋃(2;+∞)