Question

Даю 50 балів
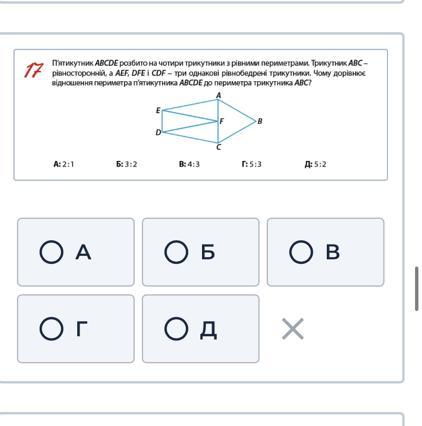
П'ятикутник ABCDE розбито на чотири трикутники з рiвними периметрами. Трикутник ABC-
рівносторонній, а AEF, DFE i CDF - три однаковi рiвнобедренi трикутники. Чому дорівнює
вiдношення периметра п'ятикутника АВСDЕ до периметра трикутника АВС?

Answer 1

Ответ:

Позначимо сторону рівностороннього трикутника ABC через a. Оскільки трикутники AEF, DFE і CDF є рівнобедреними, то їхні бічні сторони мають довжину a, тобто вони також є рівносторонніми трикутниками.

Нехай периметр п'ятикутника ABCDE дорівнює P, а периметр трикутника ABC дорівнює 3a. Тоді периметр кожного з трикутників AEF, DFE і CDF також дорівнює 2a + DE.

Отже, маємо:

P = 3a + 2a + DE + 2a + DE + 2a + DE

P = 9a + 3DE

Так як усі чотири трикутники мають рівні периметри, то:

3a + DE = 2a + 2DE

a = DE

Отже, маємо:

P = 9a + 3DE = 12DE

І відношення периметра п'ятикутника АВСDЕ до периметра трикутника АВС дорівнює:

P/3a = 4DE/3a = 4/3

Отже, відношення периметра п'ятикутника АВСDЕ до периметра трикутника АВС дорівнює 4/3.