Предмет: Алгебра,
автор: dmitrorog
Даю 50 балів, обов'язково з розв'язанням, буду вдячний
Приложения:
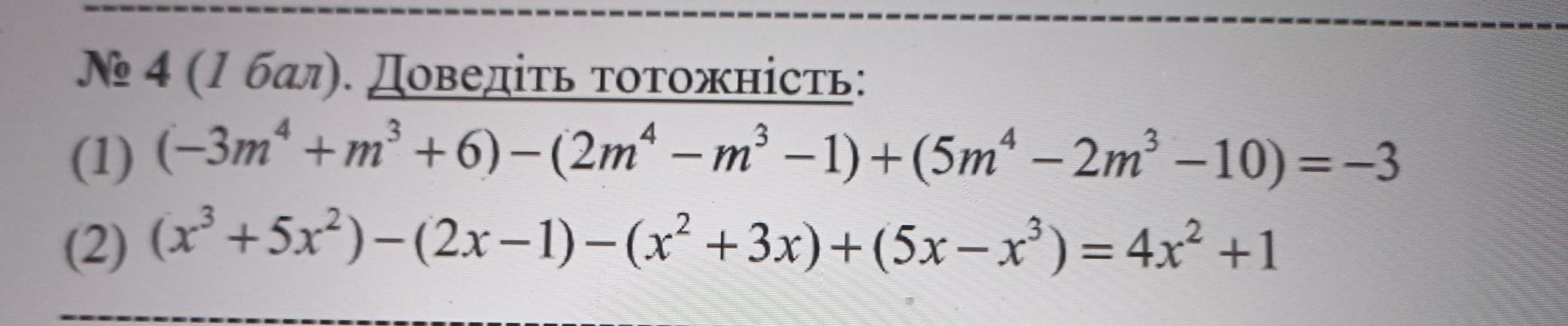
Ответы
Автор ответа:
0
Ответ:
1) (-3m⁴+m³+6) - (2m⁴-m³-1)+(5m⁴-2m³-10)= -3;
(-3m⁴+m³+6) - (2m⁴-m³-1)+(5m⁴-2m³-10)= -3m⁴+m³+6 - 2m⁴+m³+1+5m⁴ - 2m³ - 10=6+1-10=7-10= -3
2) (x³+5x²) - (2x - 1) - (x²+3x)+(5x - x³)=4x²+1;
(x³+5x²) - (2x - 1) - (x²+3x)+(5x - x³)=x³+5x² - 2x+1 - x² - 3x+5x - x³= 4x²+1
Объяснение:
При приведении подобных переменные уничтожаются и выражение упрощается до выражения в правой части
Похожие вопросы
Предмет: Математика,
автор: pisarenkonatalia693
Предмет: Русский язык,
автор: gerbernatasa2
Предмет: Английский язык,
автор: zlatachka16
Предмет: Химия,
автор: kateryna39
Предмет: Информатика,
автор: Irismoj