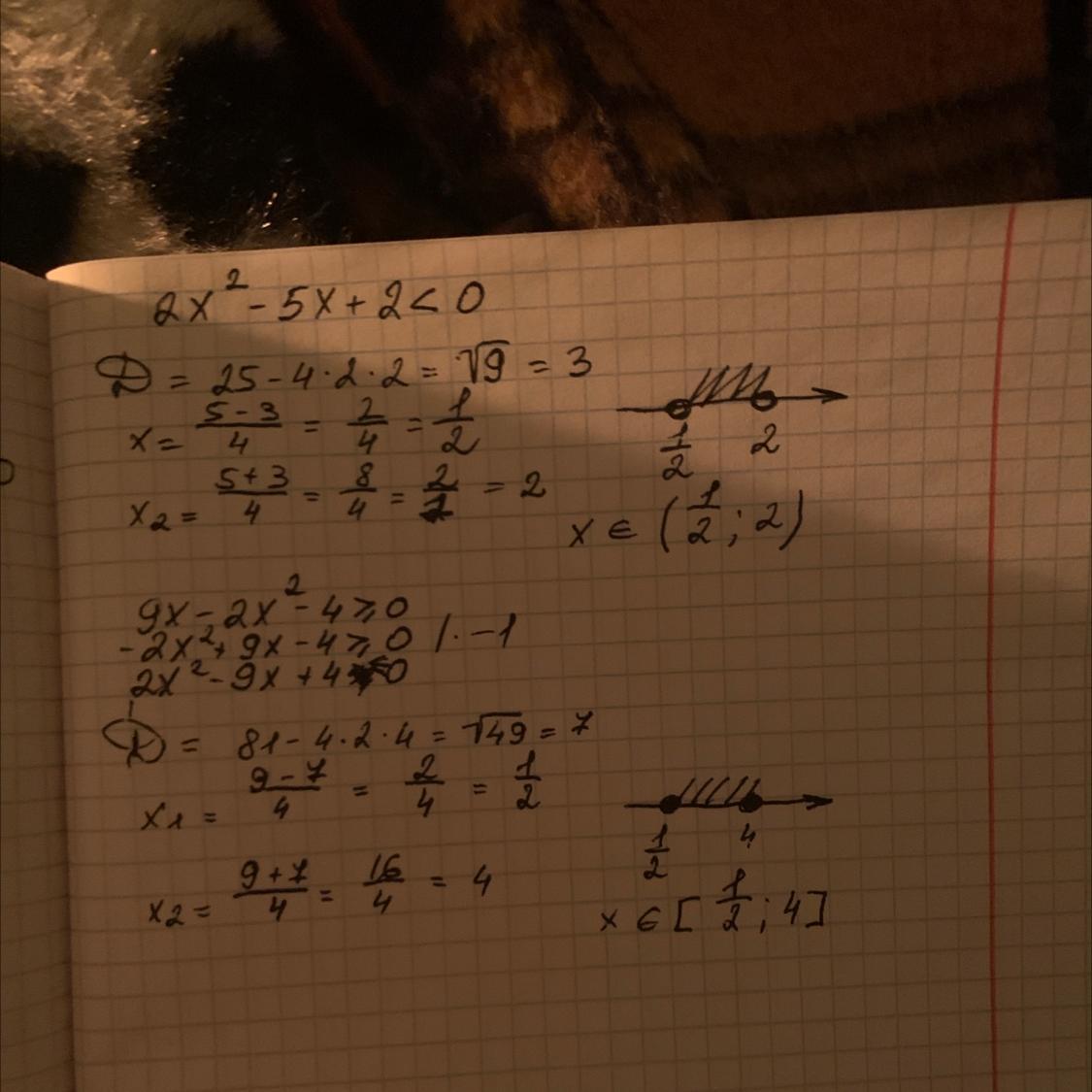Question

Знайдіть усі цілі розв'язки нерівності:
2х²- 5х + 2 < 0
9х - 2х² - 4>=0

Answer 1

Ответ:

Для вирішення квадратних нерівностей спочатку треба знайти корені відповідного квадратного рівняння.

2х² - 5х + 2 < 0:

Рівняння має вигляд: 2х² - 5х + 2 = 0

Застосуємо формулу квадратного кореня:

D = b² - 4ac = (-5)² - 4 * 2 * 2 = 25 - 16 = 9

x1,2 = (-b ± √D) / 2a

x1 = (5 + √9) / 4 = (5 + 3) / 4 = 8 / 4 = 2

x2 = (5 - √9) / 4 = (5 - 3) / 4 = 2 / 4 = 1/2

Оскільки коефіцієнт a > 0, парабола відкривається вгору, отже, нерівність задовольняється між коренями:

1/2 < x < 2

9х - 2х² - 4 >= 0:

Спочатку варто спростити вираз: -2х² + 9х - 4 >= 0

Рівняння має вигляд: -2х² + 9х - 4 = 0

Застосуємо формулу квадратного кореня:

D = b² - 4ac = 9² - 4 * (-2) * (-4) = 81 - 32 = 49

x1,2 = (-b ± √D) / 2a

x1 = (-9 + √49) / (-4) = (-9 + 7) / (-4) = -2 / (-4) = 1/2

x2 = (-9 - √49) / (-4) = (-9 - 7) / (-4) = 16 / 4 = 4

Оскільки коефіцієнт a < 0, парабола відкривається вниз, отже, нерівність задовольняється за межами інтервалу між коренями:

x <= 1/2 або x >= 4

Відповідь:

1/2 < x < 2

x <= 1/2 або x >= 4

Answer 2

Все на фото
_________