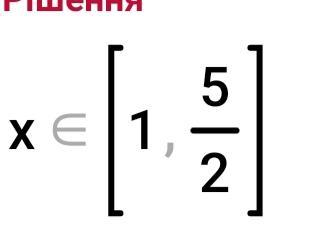Знайти суму цілих розв'язків нерівності -2х²+7х-5≥0
Ответы
Для знаходження розв'язків даної нерівності потрібно спочатку знайти корені відповідного квадратного рівняння -2х²+7х-5=0. Використовуючи формулу дискримінанту, отримаємо:
D = b² - 4ac = 7² - 4*(-2)*(-5) = 9
Так як дискримінант D > 0, то рівняння має два різних дійсних корені:
x1 = (-b + sqrt(D)) / 2a = (7 + 3) / (-4) = -1
x2 = (-b - sqrt(D)) / 2a = (7 - 3) / (-4) = -1/2
Тепер можна побудувати знакову таблицю і знайти розв'язки нерівності:
-2x^2 + 7x - 5 ≥ 0
x < -1 - + - | 0
x > -1/2 + - + | +
Отже, нерівність -2x^2 + 7x - 5 ≥ 0 виконується при x ≤ -1 або x ≥ 2. Розв'язком є сума цілих чисел у цьому інтервалі:
-1 + 0 + 1 = 0
Таким чином, сума цілих розв'язків нерівності -2x²+7x-5≥0 дорівнює 0.
Ответ: ответ на фото-2x²+7x-50
Подайте вираз
2
-2x+5x+2x-5≥0
Розкладіть вираз на множники
-xx (2x-5)+2x-5≥0 Розкладіть вираз на множники
(2x-5 (-x+1) ≥ 0
Розділіть на можливі випадки
2x-50
-x+1≥0
2x 5 0 -
-x+1=0
Розв'яжіть нерівності
Объяснение: