Question

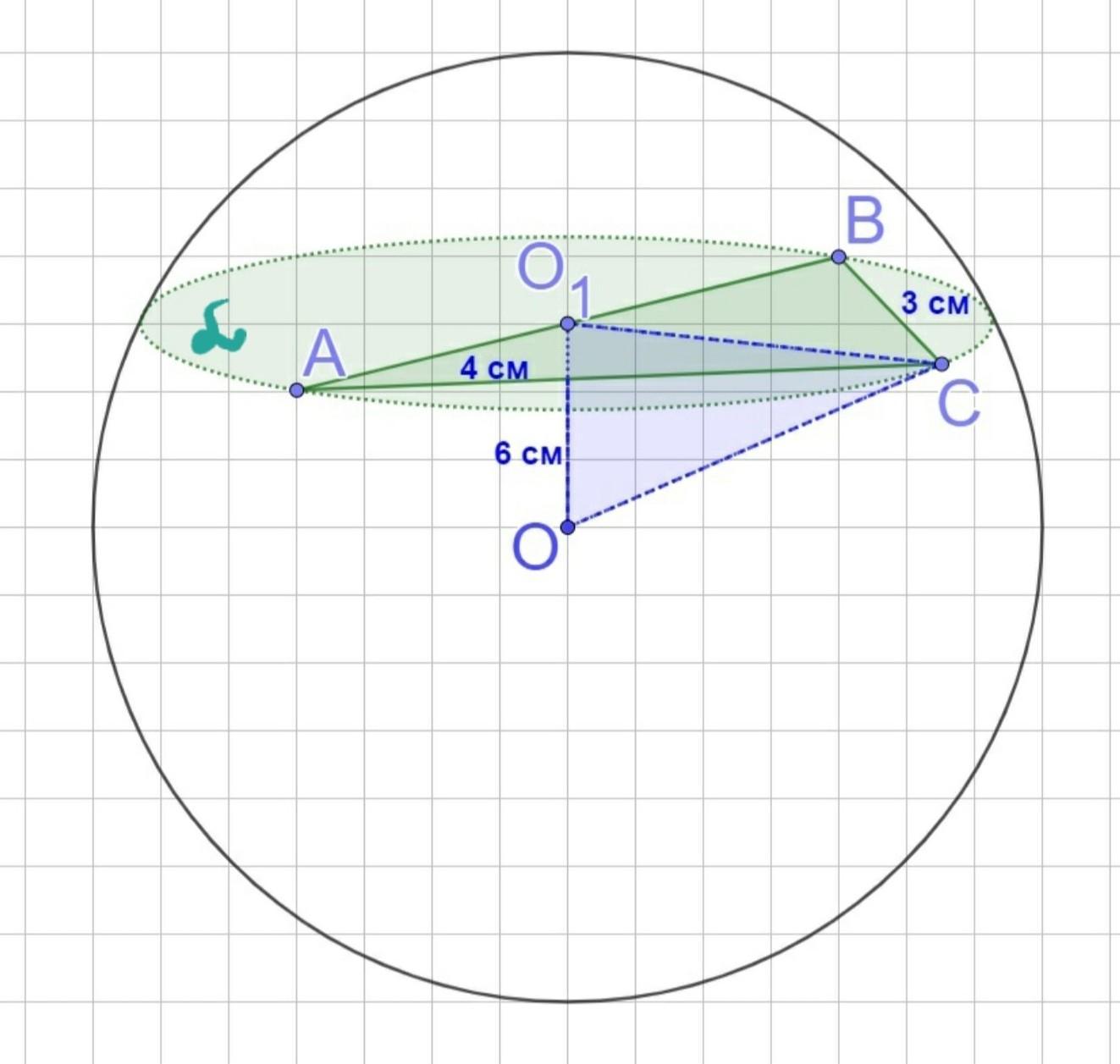
Усі вершини прямокутного трикутника з катетами 3 см і 4 см лежать на сфері .Відстань від центра сфери до площини трикутника дорівнює 6 см. Знайдіть площу поверхні сфери.

Answer 1

Ответ:

Площа поверхні сфери дорівнює 169 π см²

Объяснение:

Усі вершини прямокутного трикутника з катетами 3 см і 4 см лежать на сфері .Відстань від центра сфери до площини трикутника дорівнює 6 см. Знайдіть площу поверхні сфери.

• Площа поверхні сфери обчислюється за формулою:

S=4πR²

R - радіус сфери

Нехай задана сфера з центром в точці О, яка проходить через усі вершини прямокутного трикутника АВС з катетами АС= 4 см, ВС=3 см, а центр сфери віддалений від площини цього трикутника на відстань 6 см.

Через вершини △АВС проведемо площину α, яка перетинає сферу по колу. Так як точки А, В, С лежать на сфері, то △АВС - вписаний в це коло. △АВС - прямокутний, тому центр цього кола, точка О₁, є серединою гіпотенузи АВ, а радіус кола дорівнює ії половині.

R=AO₁=O₁B=O₁C=½•AB.

1) З прямокутного трикутника АВС(∠C=90°) за теоремою Піфагора знайдемо гіпотенузу АВ:

$AB = \sqrt{ {AC}^{2} + {BC}^{2} } = \sqrt{ {4}^{2} + {3}^{2} } = \sqrt{16 + 9} = \bf 5$ (см)

2) Тоді R=AO₁=O₁B=O₁C=AB:2=5:2=2,5(см)

3) Оскільки ОО₁⟂(АВС), то ∠ОО₁С=90°.

З △OO₁C(∠O₁=90°) за теоремою Піфагора знайдемо гіпотенузу ОС (радіус кулі)

$OC = \sqrt{ {OO_1}^{2} + {O_1C}^{2} } = \sqrt{ {6}^{2} + {2,5}^{2} } = \\ \\ = \sqrt{36 + 6,25} = \sqrt{42,25} = \bf 6,5 (cm)$

4) Знайдемо площу поверхні сфери:

S=4π•(6,5)²=4π•42,25= 169π (см²)

Відповідь: 169π см²

#SPJ1