Предмет: Алгебра,
автор: soulgamercostellano
Решить уравнение касательной
Приложения:
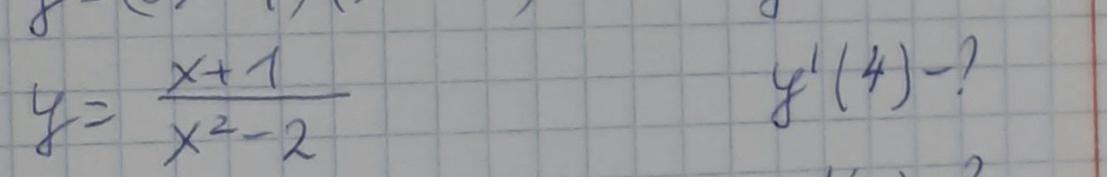
Ответы
Автор ответа:
1
Ответ:
Угловой коэффициент касательной при х₀=4 равен k=-13/98 .
Уравнение касательной : .
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Химия,
автор: bogdantonuk
Предмет: Математика,
автор: andreyka2324
Предмет: Қазақ тiлi,
автор: leno4ka69
Предмет: Русский язык,
автор: moroororejf2j