Question

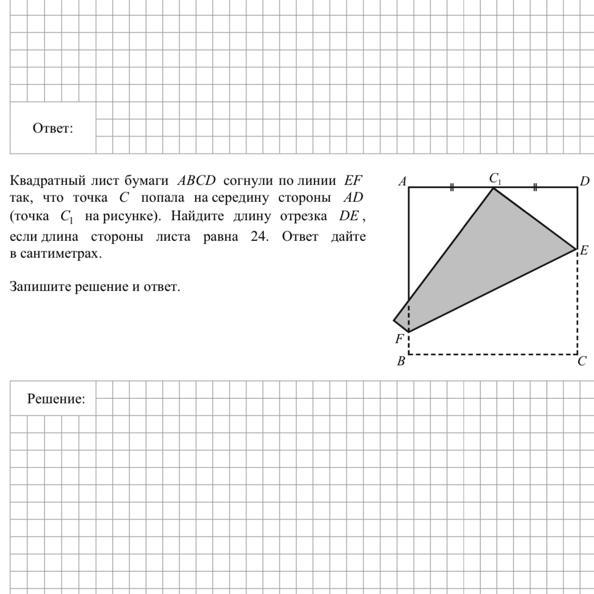
Квадратный лист бумаги ABCD согнули по линии EF A
так, что точка C попала насередину стороны AD
(точка С1 на рисунке). Найдите длину отрезка DE ,
еслидлина стороны листа равна 24. Ответ дайте в сантиметрах.
Запишите решение и ответ.

Answer 1

Ответ:

Длина отрезка DE равна 9 см.

Объяснение:

Квадратный лист бумаги ABCD согнули по линии EF так, что точка С попала на середину стороны AD (точка С₁ на рисунке). Найдите длину отрезка DE, если длина стороны листа равна 24. Ответ дайте в сантиметрах.

Дано: ABCD - квадрат;

ВС = 24 см;

АС₁ = С₁D.

Найти: DE

Решение:

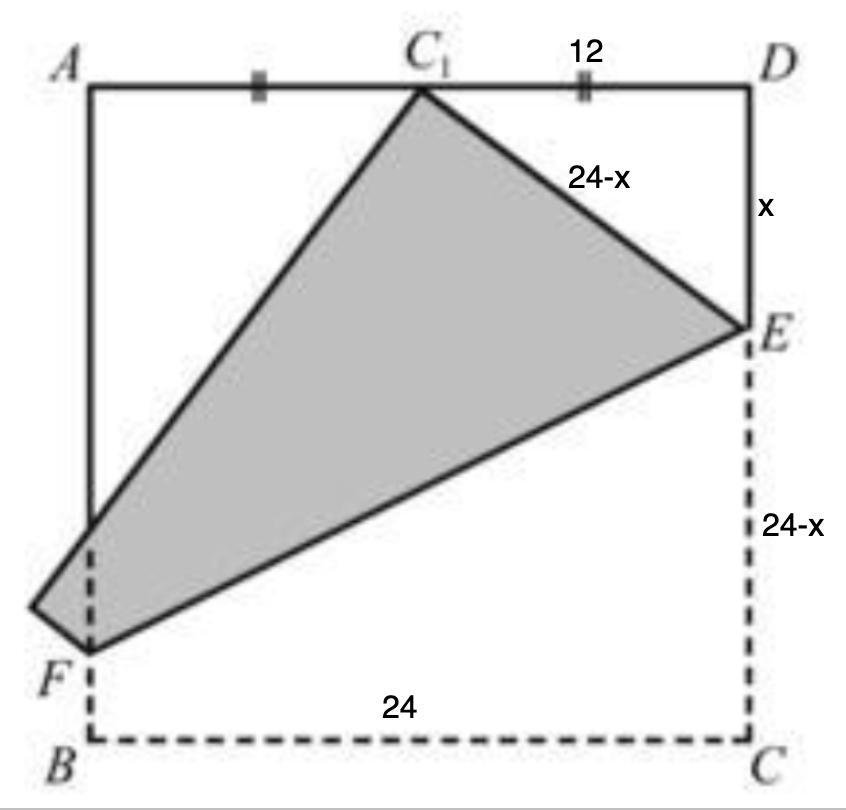
Пусть DE = x см, тогда ЕС = (24 - х) см

С₁Е = ЕС = (24 - х) см

Рассмотрим ΔС₁DE - прямоугольный.

C₁D = 24 : 2 = 12 (см); DE = x см; С₁Е = (24 - х) см

• Используем теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

EC₁² = C₁D² + DE²

(24 - х)² = 144 + х²

576 - 48х + х² = 144 + х²

-48х = 144 - 576

-48х = - 432     |: (-48)

x = 9

Длина отрезка DE равна 9 см.

#SPJ1