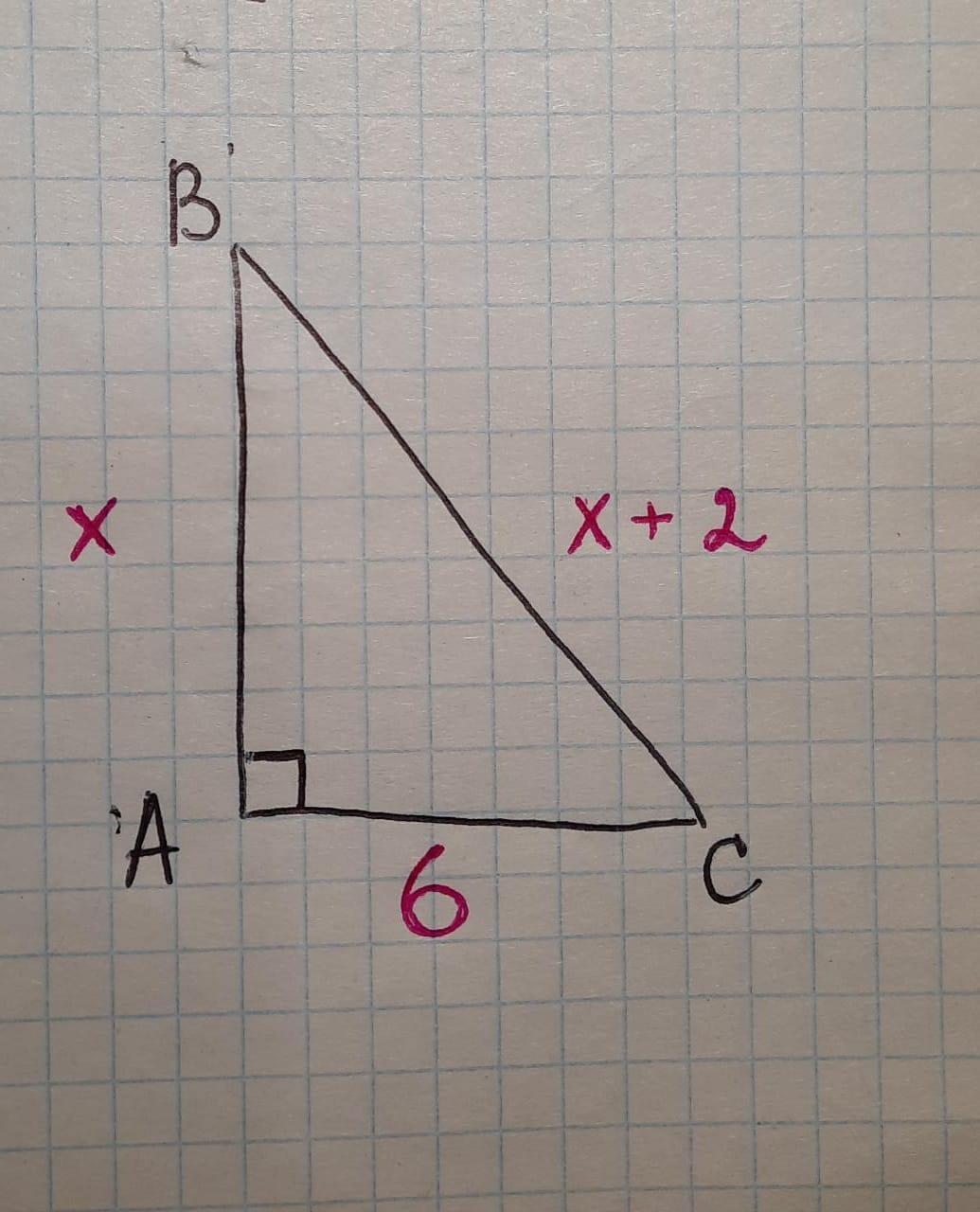ПОМОГИТЕ ПОЖАЛУЙСТА
В прямоугольном треугольнике гипотенуза больше одного из катетов на 2 см, а второй катет равен 6 см. Вычислите угол, лежащий против меньшего катета.
Ответы
1)
Введем обозначения: первый катет (ВА) = Х см
второй катет (АС) = 6 см
гипотенуза (ВС) = (Х + 2) см
2)
т.к. △ прямоугольный, то по т.Пифагора ВA² +АС² = ВC²
подставим наши данные Х²+6² = (Х+2)²
Х²+6² = Х² + 4Х + 4
Х² - Х² - 4Х = -6² + 4
- 4Х = -36 + 4
- 4Х = -32
Х = 8 см - первый катет (ВА)
тогда (Х+ 2) = 8+2 = 10 см - гипотенуза (ВС)
3)
Зная все три стороны треугольника: АС = 6 см
BA = 8 см
ВС = 10 см
найдем ∠С = cos(AC/BC) = cos(6/10) = cos(0,6) = 53°
4)
∠B = 180° - ∠A - ∠С = 180° - 90° - 53° = 37°
ОТВЕТ: ∠B = 37°