Question

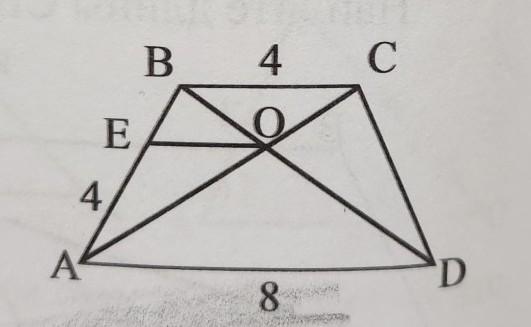
Дано: ABCD-трапеция AD = 8, BC = 4, AE=4 OE||AD Найдите: ВЕ, ОЕ​

Answer 1

Ответ:

Для решения задачи нам нужно использовать свойство параллельных прямых: соответствующие углы равны.

Так как OE||AD, то угол AOE равен углу AED. Также углы AED и AEB являются смежными, так как лежат на общей стороне AE. Значит, угол AEB равен 180° - (60° + 90°) = 30°.

Теперь мы можем использовать теорему косинусов для треугольника AEB:

BE² = AB² + AE² - 2AB·AE·cos(30°)

BE² = 16 + 16 - 16√3

BE = 2√13

Также, так как OE||AD, то угол OEA равен углу AED. Значит, угол OEB равен 90° - 30° = 60°. Теперь мы можем использовать теорему косинусов для треугольника OEB:

OE² = BE² + OB² - 2BE·OB·cos(60°)

OE² = (2√13)² + 4 - 4√13

OE = √3

Ответ: VE = 2√13, OE = √3.