помогите пожалуйста
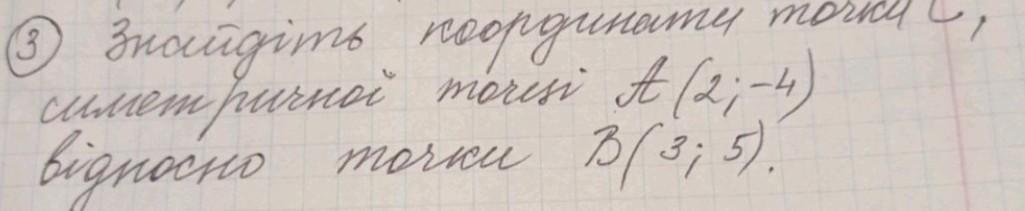
Ответы
Объяснение:
Спочатку знайдемо відрізок AB:
AB = [(3-2)^2 + (5-(-4))^2]^(1/2) = [1 + 81]^(1/2) = 8.
Точка B є серединою відрізка AC, тому AC = 2AB = 16.
Також відрізок AB має напрямок від точки A до точки B. Пряма, яка проходить через точки A та B, має рівняння:
y - 5 = (-4 - 5) / (2 - 3) * (x - 3)
y - 5 = 9(x - 3)
y = 9x - 22
Знайдемо точку C, віддаль якої від B дорівнює AC, або 16 одиниць. Нехай координати точки C дорівнюють (x, y):
[(x - 3)^2 + (y - 5)^2]^(1/2) = 16
Також точка C має лежати на прямій y = 9x - 22:
y = 9x - 22
Підставимо y з другого рівняння в перше:
[(x - 3)^2 + (9x - 27)^2]^(1/2) = 16
Розв'яжемо рівняння за допомогою підстановки t = x - 3:
[t^2 + (9t - 9)^2]^(1/2) = 16
t^2 + 81t^2 - 162t + 81 = 256
82t^2 - 162t - 175 = 0
t^2 - 2t - 2.1341 = 0
Розв'язавши квадратне рівняння, отримуємо два значення t: t1 = 2 + (8.1341)^(1/2) та t2 = 2 - (8.1341)^(1/2).
Підставимо значення t у вираз x = t + 3, щоб знайти дві координати для точки C:
x1 = 2 + (8.1341)^(1/2) + 3 = 5 + (8.1341)^(1/2)
y1 = 9x1 - 22
x2 = 2 - (8.1341)^(1/2) + 3 = 5 - (8.1341)^(1/2)
y2 = 9x2 - 22
Таким чином, координати точок C1 та C2 є:
C1: (5 + (8.1341)^(1/2), 9(5 + (8.1341)^(1/2)) - 22)
C2: (5 - (8.1341)^(1/2), 9(5 - (8.1341)^(1/2)) - 22)
Перевіримо знайдені точки:
- Відстань від точки B до C1 дорівнює 16, оскільки вона є симетричною відносно точки B точки A. Відстань від точки B до C2 також дорівнює 16, тому обидві знайдені точки є вірними розв'язками.
Отже, координати симетричної точки C відносно точки B є: C1 (5 + (8.1341)^(1/2), 17.659) або C2 (5 - (8.1341)^(1/2), -4.659).