С-4 ЕгЭ
Найти объем правильной треугольной пирамиды, у которой плоский угол при вершине равен 90 град, а расстояние между боковым ребром и противоположной стороной основания равно d.
РЕШЕНИЕ и РИСУНОК
Ответы
По условию, BS ┴SA и BS ┴SC , т.е. BS -перпендикуляр к грани SAC и SD = d.
Следовательно, искомый объем V=1/3*S(ACS)*BS.
В треуг. SAD имеем <SDA =90, <ASD =45, откуда AD=SD=d и S(ACS) = d^2.
Далеe, в треуг.BSD имеем <BSD =90, BD=2d*√3/2=d√3 ,
откуда BS=√(BD^2-SD^2)=√(3d^2-d^2)=d√2.
Окончательно находим V=1/3*d^2*d√2=1/3*d^3√2
Ответ V=d^3√2/3
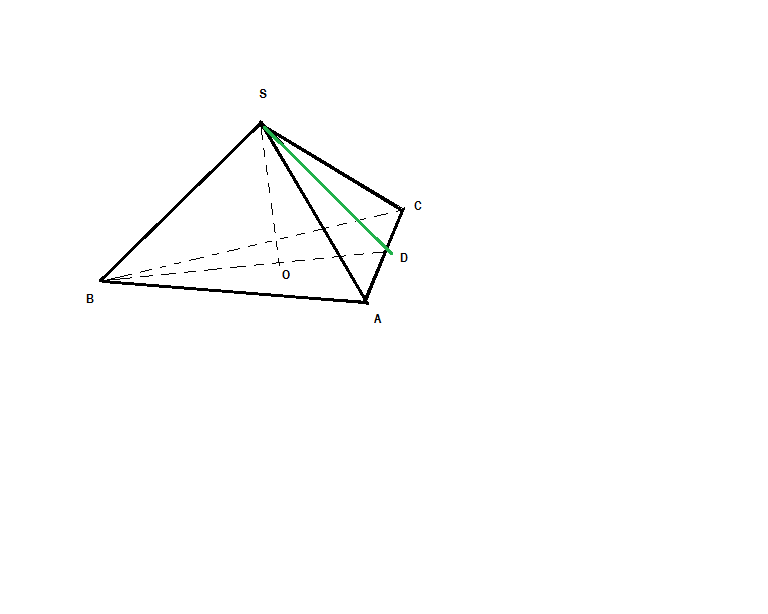
По условию, BS ┴SA и BS ┴SC , т.е. BS -перпендикуляр к грани SAC и SD = d.
Следовательно, искомый объем V=1/3*S(ACS)*BS.
В треуг. SAD имеем <SDA =90, <ASD =45, откуда AD=SD=d и S(ACS) = d^2.
Далеe, в треуг.BSD имеем <BSD =90, BD=2d*√3/2=d√3 ,
откуда BS=√(BD^2-SD^2)=√(3d^2-d^2)=d√2.
Окончательно находим V=1/3*d^2*d√2=1/3*d^3√2
