СРОЧНО
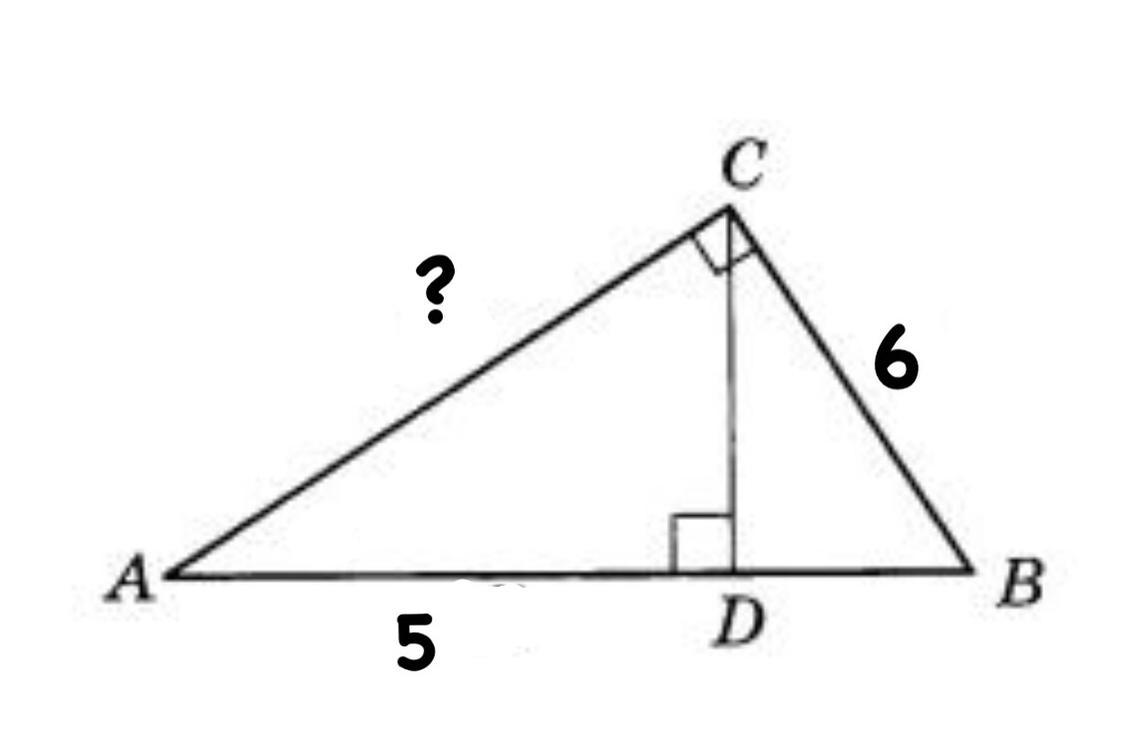
один з катетів прямокутного трикутника дорівнює 6 см а проекція другого катета на гіпотенузу дорівнює 5 см. Знайти другий катет
Ответы
a^2 + b^2 = c^2,
де a і b - катети, а c - гіпотенуза.
Підставляємо відомі значення:
6^2 + b^2 = c^2
Також відомо, що проекція другого катета на гіпотенузу дорівнює 5 см, тому:
b^2 = 5^2 = 25
Підставляємо це значення:
6^2 + 25 = c^2
Розв'язуємо:
c^2 = 61
c = sqrt(61) (корінь з 61)
Отже, довжина гіпотенузи дорівнює sqrt(61) см.
Застосовуючи теорему Піфагора знову, знаходимо другий катет:
a^2 + b^2 = c^2
6^2 + b^2 = (sqrt(61))^2
b^2 = (sqrt(61))^2 - 6^2
b^2 = 61 - 36
b^2 = 25
b = 5 (бо довжина сторони не може бути від'ємною)
Отже, другий катет дорівнює 5 см.
Дано:
CB = 6 см
AD = 5 см
AC - ?
Розв'язок:
Позначимо AC як x.
Cкладемо рівняння:
x / (гіпотенуза) = (проекція катета) / (гіпотенуза)
x / c = 5 / c, де c - довжина гіпотенузи.
x = 5c / 6
Підставляємо вираз для c, використовуючи теорему Піфагора:
, де a і b - довжини катетів, c - довжина гіпотенузи.
Розв'язуємо для x:
Обчислюємо значення x:
≈ 5.78 см.
Відповідь: AC ≈ 5.78 см.