Из пункта A выехал велосипедист со скоростью 5 м/с. Через 20 минут навстречу ему из пункта В, находящегося на расстоянии 15 км от А, выехал автомобиль со скоростью 54 км/ч. Велосипедист на середине пути сделал привал в течение 5 мин и продолжил движение до пункта В.
По какому закону изменялось расстояние между ними с момента начала движения велосипедиста и до момента прибытия автомобиля в пункт А?
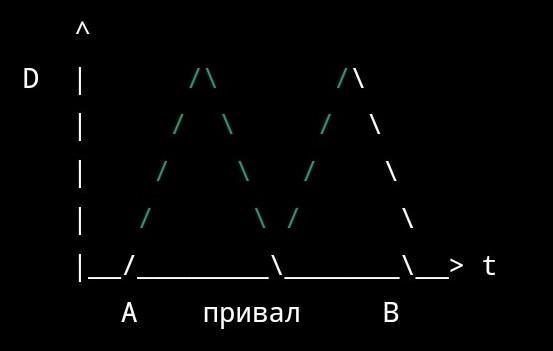
Постройте график этой зависимости.
Ответы
Ответ:
Расстояние между пунктом А и В можно обозначить буквой D.
Находим время движения автомобиля:
20 минут = 20/60 = 1/3 часа - время, за которое велосипедист проехал часть пути до места привала
5 минут = 5/60 = 1/12 часа - время, которое велосипедист простоял на месте привала
Оставшееся время для автомобиля: 1 - (1/3 + 1/12) = 5/12 часа
Теперь можем найти расстояние между автомобилем и пунктом А в момент, когда велосипедист сделал привал:
D1 = 54 км/ч * 5/12 ч = 22.5 км
Расстояние, которое нужно проехать велосипедисту до пункта В после места привала:
D2 = D - 15 км = 15 км
Время, за которое велосипедист проехал оставшуюся часть пути:
t = D2 / v, где v - скорость велосипедиста
v = 5 м/с * 3.6 = 18 км/ч
t = D2 / v = (15 км) / (18 км/ч) = 5/6 часа
Теперь можем найти расстояние между велосипедистом и пунктом В:
D3 = v * t = (18 км/ч) * (5/6 ч) = 15 км
Таким образом, вся дистанция D между пунктами А и В равна:
D = D1 + D2 + D3 = 22.5 км + 15 км + 15 км = 52.5 км
Закон изменения расстояния между велосипедистом и автомобилем можно выразить графически. Расстояние между ними увеличивается до момента, когда велосипедист делает привал, а затем уменьшается до того, как они встретятся в пункте В.
График будет выглядеть примерно так: