Предмет: Математика,
автор: DmitriyVasapen
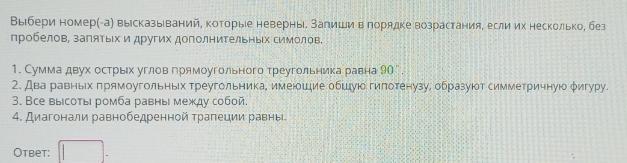
Даю 35 баллов, помогите пожалуйста!
Приложения:
Ответы
Автор ответа:
1
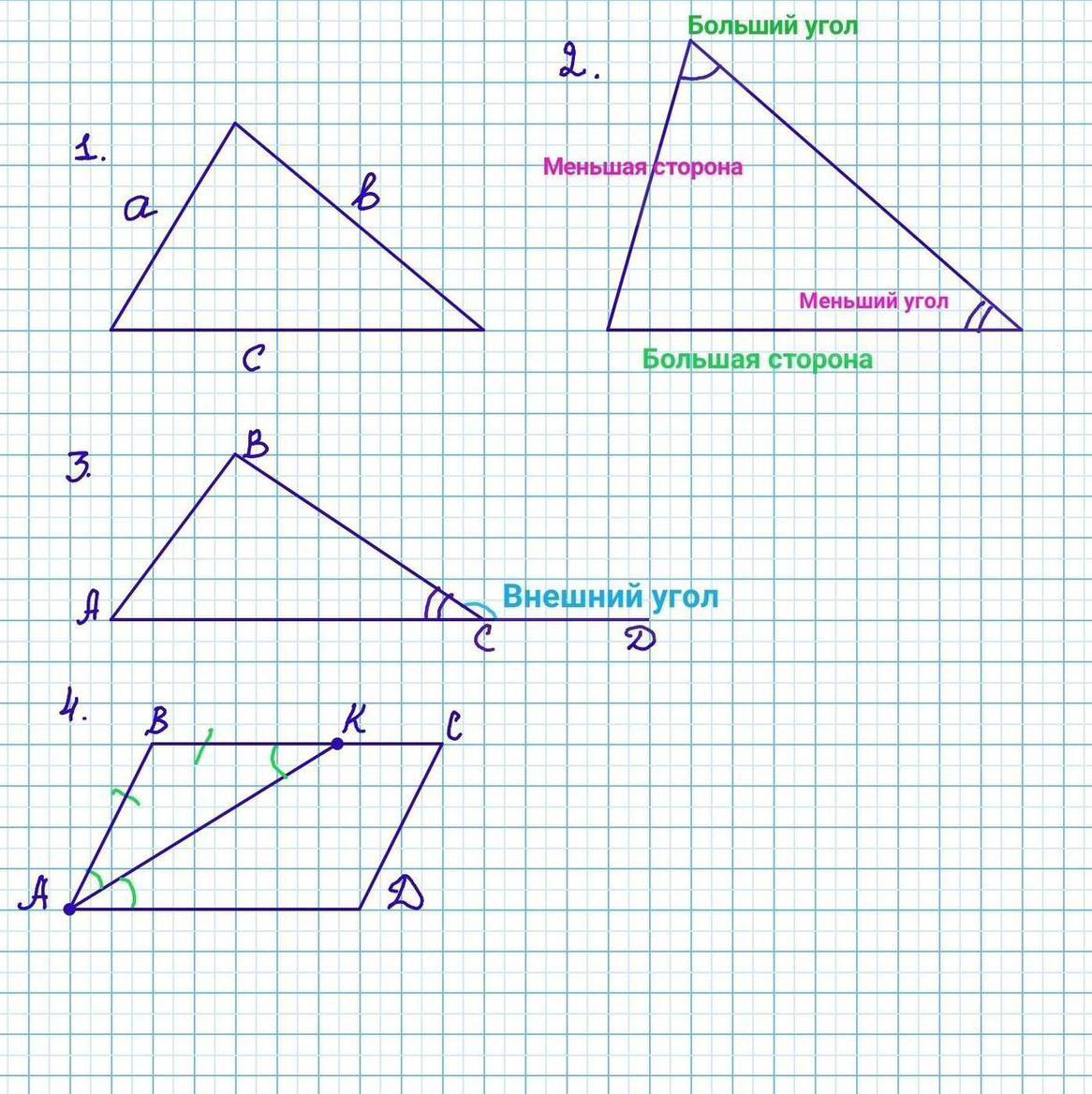
• Сумма 2-х сторон обязательно больше третьей. - Верно
Существует теорема: Сумма длин двух любых сторон больше длины третьей стороны этого . (a + b > c, b+c > a, a+c > b).
•Напротив острого угла обязательно лежит самая маленькая его сторона. - Неверно
Существует теорема: в против меньшей стороны лежит меньший угол, против большей - больший угол.
В остоугольном все углы острые, и напротив одного из этих острых углов необязательно лежит самая маленькая сторона.
К примеру, напротив большего острого угла лежит самая большая сторона.
•Внешний угол меньше 180°. - Верно
Внешний угол – это угол, смежный с любым из внутренних углов .
Сумма смежных углов равна 180°, следовательно внутренний угол всегда меньше 180°.
∠ACB+∠BCD=180°. ∠BCD=180°-∠ACB.
•Если провести биссектрису из угла параллелограмма, то она отсечёт равнобедренный . - Верно
Рассмотрим параллелограмм ABCD. AK - биссектриса. ∠BAK =∠KAD - по свойству биссектрисы.
Но ∠KAD= ∠BKA, как внутренние накрест лежащие углы при параллельных прямых ВС и AD и секущей АК. Следовательно ∠BAK=∠BKA.
А если углы при основании равны, то равнобедренный.
△АВК - равнобедренный.
Существует теорема: Сумма длин двух любых сторон больше длины третьей стороны этого . (a + b > c, b+c > a, a+c > b).
•Напротив острого угла обязательно лежит самая маленькая его сторона. - Неверно
Существует теорема: в против меньшей стороны лежит меньший угол, против большей - больший угол.
В остоугольном все углы острые, и напротив одного из этих острых углов необязательно лежит самая маленькая сторона.
К примеру, напротив большего острого угла лежит самая большая сторона.
•Внешний угол меньше 180°. - Верно
Внешний угол – это угол, смежный с любым из внутренних углов .
Сумма смежных углов равна 180°, следовательно внутренний угол всегда меньше 180°.
∠ACB+∠BCD=180°. ∠BCD=180°-∠ACB.
•Если провести биссектрису из угла параллелограмма, то она отсечёт равнобедренный . - Верно
Рассмотрим параллелограмм ABCD. AK - биссектриса. ∠BAK =∠KAD - по свойству биссектрисы.
Но ∠KAD= ∠BKA, как внутренние накрест лежащие углы при параллельных прямых ВС и AD и секущей АК. Следовательно ∠BAK=∠BKA.
А если углы при основании равны, то равнобедренный.
△АВК - равнобедренный.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: iliasdinara0571
Предмет: Литература,
автор: vusmatvii2008
Предмет: Русский язык,
автор: ddarinaa90
Предмет: Физика,
автор: ramilpovarov228