Question

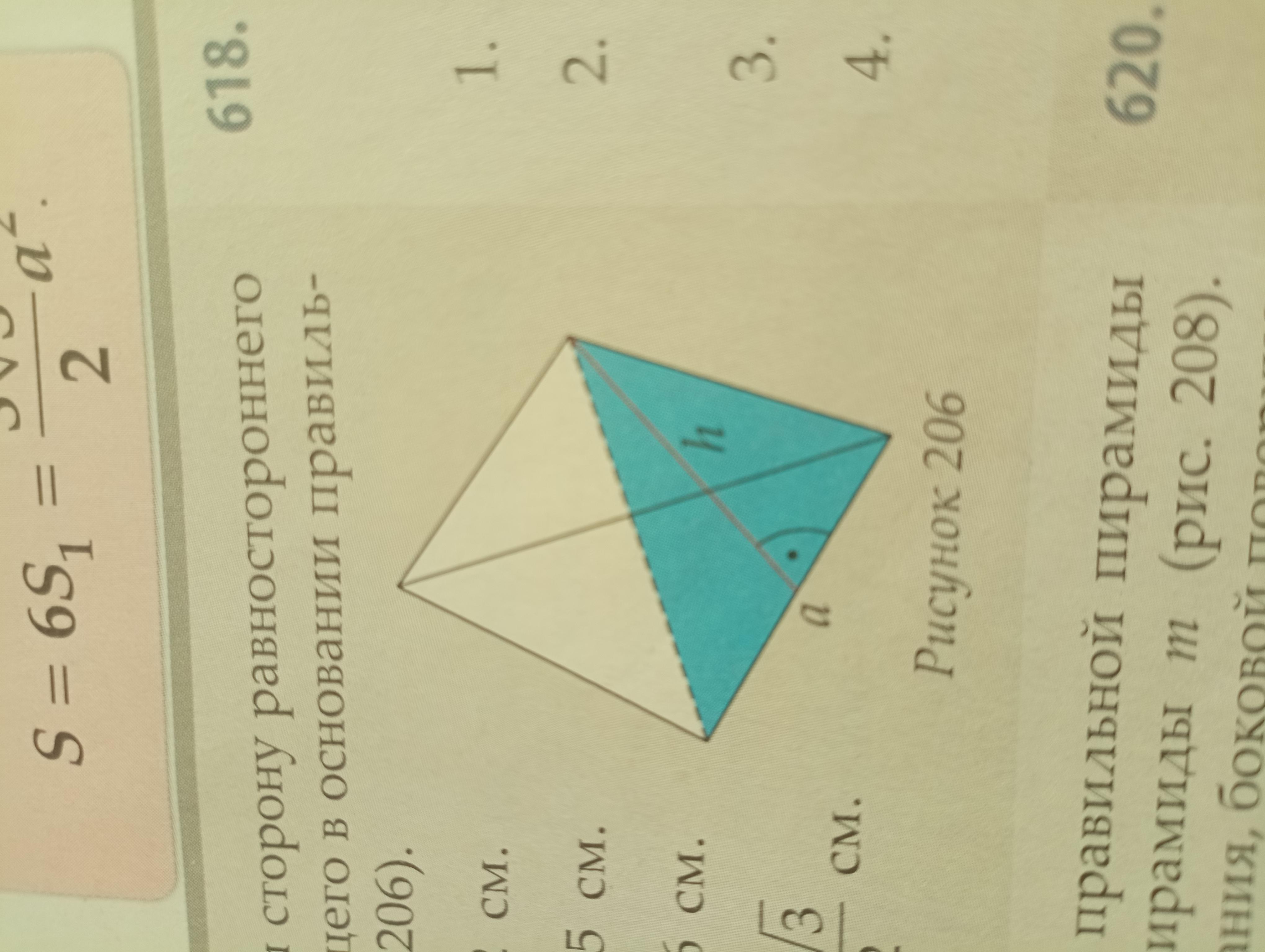
Вычисли высоту или сторону равностороннего треугольника,лежавщего в основании правильной пирамиды если а=45 см

Answer 1

Ответ:

Для решения задачи необходимо знать свойства правильной пирамиды. Одно из таких свойств - высота правильной пирамиды делит её боковые грани на равнобедренные треугольники, основания которых равны боковому ребру пирамиды.

Таким образом, в правильной пирамиде, если её боковые грани - равнобедренные треугольники с основанием a, то её боковое ребро равно a, а высота равна h = a * sqrt(3) / 2.
В данном случае, известно, что a = 45 см, следовательно, высота h равна:
h = a * sqrt(3) / 2 = 45 * sqrt(3) / 2 ≈ 38.93 см
Ответ: высота равностороннего треугольника, лежащего в основании правильной пирамиды, равна примерно 38.93 см.