Предмет: Алгебра,
автор: fishermiraacer
Помогите решить пожалуйста !!!! Даю 100 баллов
Приложения:
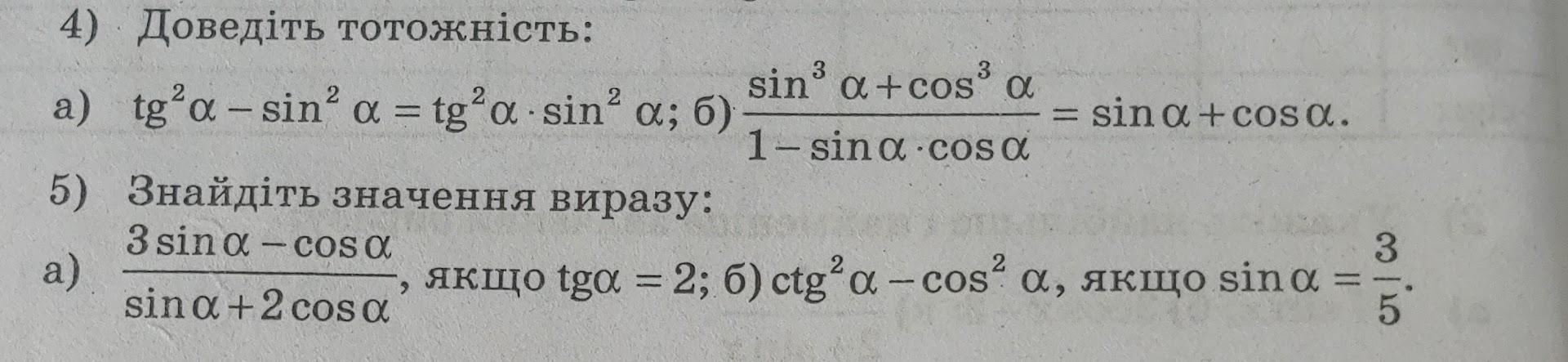
Ответы
Автор ответа:
2
Ответ:
Применяем тригонометрические тождеcтва : .
4) Доказать тождество .
5) Найти значение выражения .
kurlic567:
https://znanija.com/task/52251497
Похожие вопросы
Предмет: Литература,
автор: gusik228229
Предмет: История,
автор: lalalalala576809
Предмет: История,
автор: storozhukangelina83
Предмет: Математика,
автор: fiat1985
Предмет: Математика,
автор: wese6886we1