Question

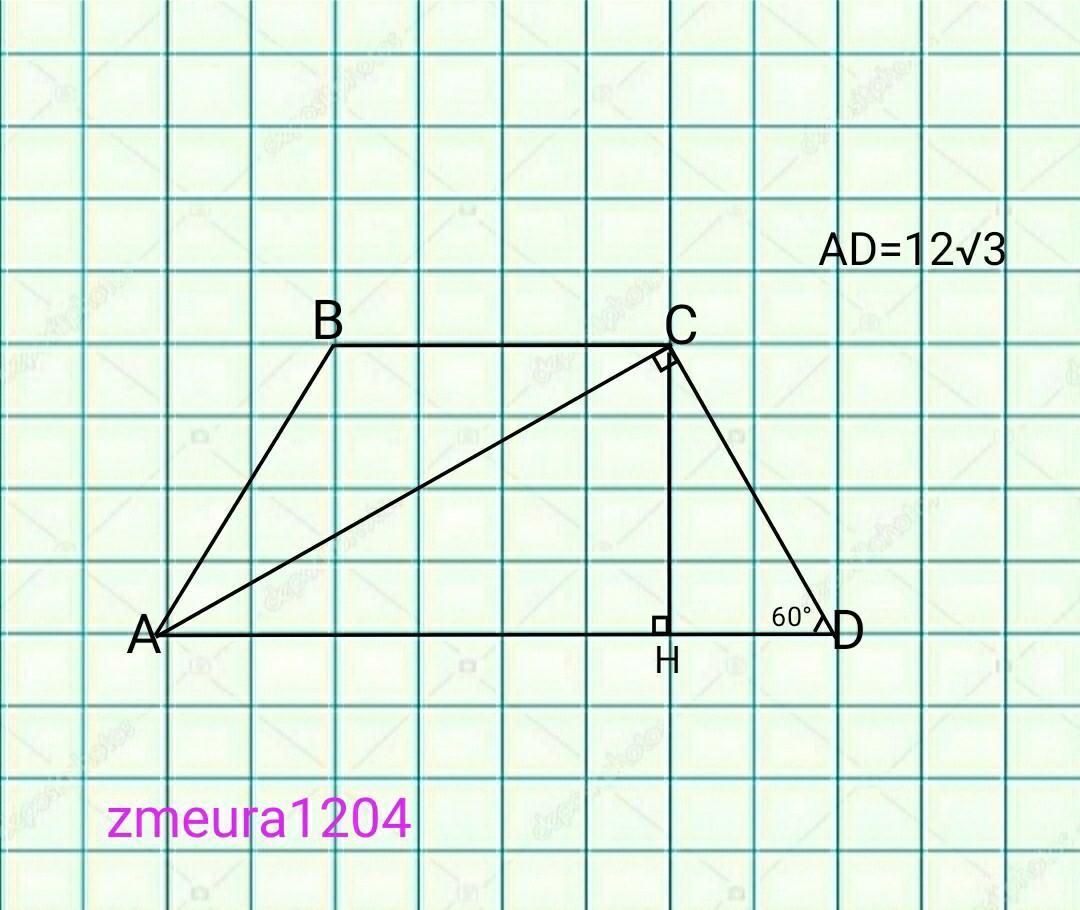
5. В равнобедренной трапеции диагональ перпендикулярна Найдите площадь трапеции, если
большее основание равно 12√3, а один из углов трапеции равен 60
боковой стороне.

Answer 1

Ответ:

S(ABCD)=81√3 ед²

Объяснение:

∆ACD- прямоугольный треугольник.

∠САD=90°-∠CDA=90°-60°=30°

CD- катет против угла 30°

CD=AD/2=12√3/2=6√3 ед.

По теореме Пифагора:

АС=√(АD²-CD²)=√((12√3)²-(6√3)²)=

=√(432-108)=√324=18 ед.

Пропорциональные отрезки прямоугольного треугольника:

СН=АС*СD/AD=18*6√3/12√3=9 ед.

CD²=HD*AD; → HD=CD²/AD=(6√3)²/12√3=

=108/12√3=3√3 ед.

ВС=АD-2*HD=12√3-2*3√3=6√3.

S(ABCD)=CH(BC+AD)/2=9(6√3+12√3)/2=

=9*18√3/2=81√3 ед²