Question

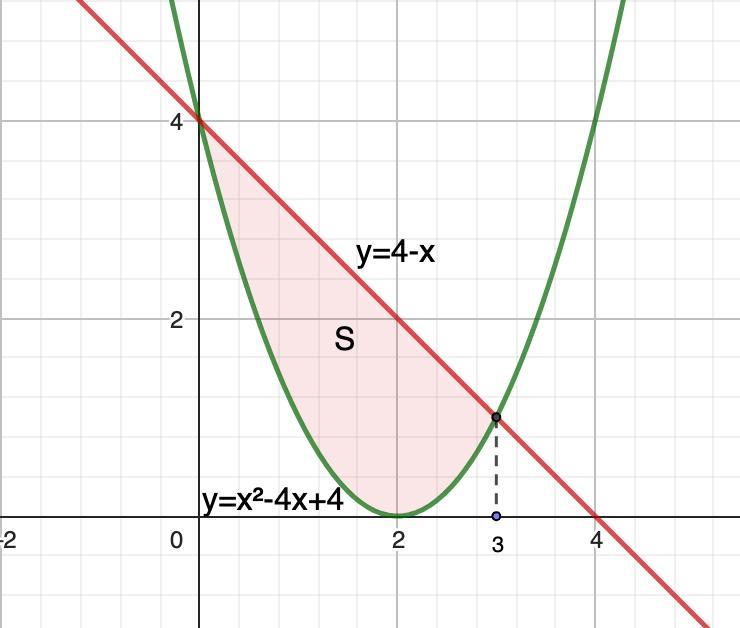
Обчислюють площу фігури, обмеженої лініями
y = x² - 4x + 4, y = 4 - х. Вказати, які з наведених
чотирьох тверджень правильні:
1) Графіки заданих функцій перетинаються в
точках з абсцисами 1 і 4
2) Для кожного значення х з проміжку (0; 3)
точка графіка функції у = 4-х знаходиться вище
відповідної точки графіка функції у = х2 4x + 4
3) Площу заданої фігури можна знайти за
формулою †((4-x)-(x² - 4x + 4))dx
4) Площа заданої фігури більша за 5

Answer 1

Ответ:

1) НЕВЕРНО. Графики пересекаются в точках с абсциссами 0 и 3.

2) ВЕРНО. (см. рис)

3) ВЕРНО. По этой формуле мы нашли площадь.

4) НЕВЕРНО. Площадь фигуры 4,5 ед.²

Объяснение:

Вычислить площадь фигуры, ограниченной линиями y = x²-4x+4, y = 4-х. указать, какие из следующих четырех утверждения верны:

1) графики заданных функций пересекаются в точках с абсциссами 1 и 4;

2) для каждого значения х из промежутка (0; 3) точка графика функции у = 4-х находится выше соответствующей точки графика функции у = х²-4x+4

3) Площадь заданной фигуры можно найти по формуле:

$\displaystyle \bf \int\limits^3_0 {((x-4)-(x^2-4x+4))} \, dx$

4) площадь заданной фигуры больше 5.

y = x²-4x+4 = (х-2)²

- парабола, ветви вверх.

Этот график получается из графика у = х² сдвигом на 2 единицы вправо.

у = 4-х

- линейная функция, график прямая.

Найдем точки пересечения этих графиков:

х² - 4х + 4 = 4 - х

х²-3х = 0

х (х - 3) = 0

х = 0;     х = 3

⇒ графики пересекаются в точках с абсциссами 0 и 3.

Найдем площадь фигуры, ограниченной данными функциями.

•                Формула:

             $\displaystyle \bf S=\int\limits^b_a {(f_2(x)-f_1(x))} \, dx$

a = 0 (слева); b = 3 (справа); f₂(x) = 4-x (сверху); f₁(x) = x²-4x+4 (снизу)

$\displaystyle S=\int\limits^3_0 {((4-x)-(x^2-4x+4))} \, dx =\int\limits^3_0 {(-x^2+3x)} \, dx =\\\\=\left(-\frac{x^3}{3}+\frac{3x^2}{2}\right)\bigg|^3_0=-\frac{27}{3}+\frac{27}{2} -0=-9+13,5=4,5$(ед.²)

Проверим, какие из следующих четырех утверждения верны:

1) графики заданных функций пересекаются в точках с абсциссами 1 и 4;

НЕВЕРНО. Графики пересекаются в точках с абсциссами 0 и 3.

2) для каждого значения х из промежутка (0; 3) точка графика функции у = 4-х находится выше соответствующей точки графика функции у = х²-4x+4.

ВЕРНО. (см. рис)

3) Площадь заданной фигуры можно найти по формуле:

$\displaystyle \bf \int\limits^3_0 {((x-4)-(x^2-4x+4))} \, dx$

ВЕРНО. По этой формуле мы нашли площадь.

4) площадь заданной фигуры больше 5.

НЕВЕРНО. Площадь фигуры 4,5 ед.²

#SPJ1