напротив меньшси 4. В равнобедренном треугольнике см. Найдите радиус вписанной ка окружности. боковая сторона равна 20 см, основание равно 52 в этот треугольник и радиус описанной около.
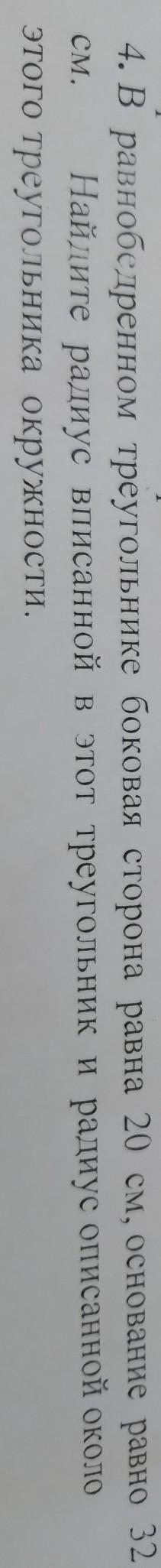
Ответы
Ответ:
Пусть R - радиус описанной окружности, r - радиус вписанной окружности. Самые известные формулы нахождения вписанной и описанной окружностей:
r=\frac{S}{p},\,\,\,\,R=\frac{abc}{4S}.
Здесь p - полупериметр треугольника, S - площадь треугольника,
a, b, c -стороны треугольника.
p=(20+20+32):2
p=20+16
p=36 см
В данном случае а=20 см, b=20 см, с=32 см.
Площадь треугольника можно найти по формуле Герона.
S=\sqrt{p(p-a)(p-b)(p-c)}. Подставим известные значения:
S=\sqrt{36(36-20)*(36-20)*(36-32)}
S=\sqrt{6^2*16^2*4}
S=\sqrt{6^2*16^2*2^2}
S=6*16*2 см²
Точное значение можно не вычислять, по условию задачи это не требуется.
Подставим известные данные в формулу вычисления радиуса вписанной окружности.
r=\frac{6*16*2}{36}
Сокращаем на 6 числитель и знаменатель
r=\frac{16*2}{6}
Сокращаем на 2 обе части. Получаем
r=\frac{16}{3}
r=5\frac{1}{3} см
Подставим известные данные в формулу вычисления радиуса описанной окружности.
R=\frac{20*20*32}{4*6*2*16}.
Делим числитель и знаменатель на 32.
R=\frac{20*20}{4*6}.
Делим числитель и знаменатель на 4.
R=\frac{5*20}{6}.
Делим числитель и знаменатель на 2:
R=\frac{5*10}{3}
R=18\frac{2}{3} см.